剑指 Offer 55 - I. 二叉树的深度

大家好，我是吴师兄。

今天继续来学习《剑指Offer》系列的一道经典题目，依旧给出了非常详细的题解和精美的配图与动画。

一、题目描述

输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

例如：

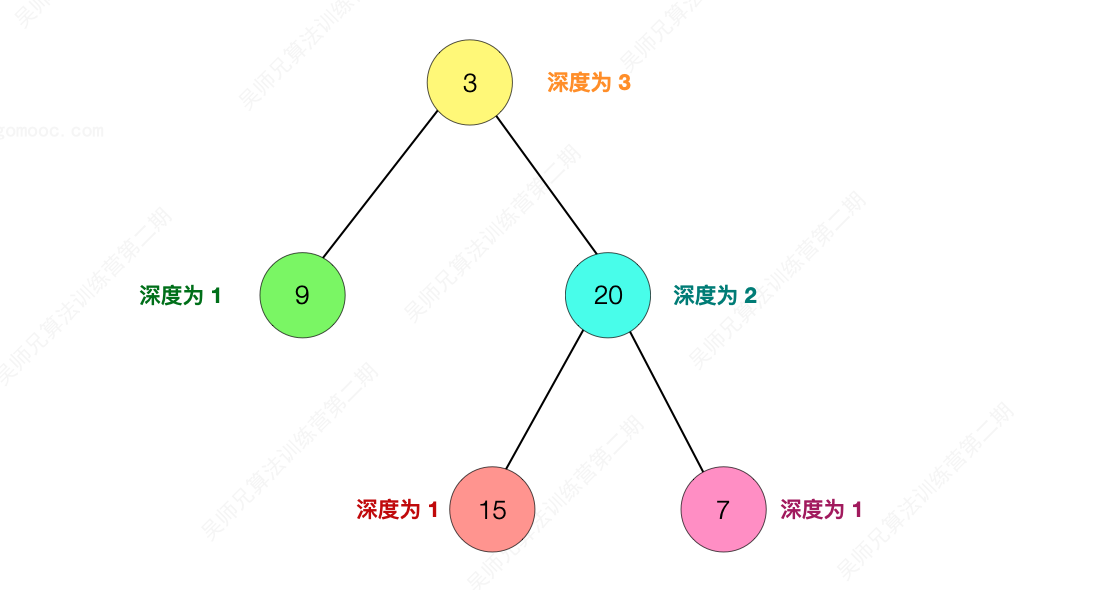
给定二叉树 [3,9,20,null,null,15,7]

    3
   / \
  9  20
    /  \
   15   7

返回它的最大深度 3 。

提示：

1. 节点总数 <= 10000

二、题目解析

题目要求我们统计二叉树的深度，对于根节点来说，它的深度取决于左子树的深度和右子树的深度。

对于左子树来说，它的深度同样取决于它的左子树的深度和右子树的深度。

对于右子树来说，它的深度同样取决于它的左子树的深度和右子树的深度。

因此，树的深度 等于 它的左子树的深度 与 它的右子树的深度 中的 最大值 +1 。

具体操作如下：

• 1、计算节点 root 的 左子树的深度
• 2、计算节点 root 的 右子树的深度
• 3、不断的递归调用 1 与 2 ，直到访问到叶子节点时，可以获取到以原来的二叉树中的叶子节点作为根节点的那棵二叉树的深度，比如 9、15、7 就是叶子节点，深度就是它们本身占据的深度，为 1。
• 4、那么节点 root 的深度就是 1 与 2 的较大值加上 1 （因为节点 root 本身也是占据了一个深度的）。

为了帮助你更好的理解整个过程，我特意做了一组动画，点开可以查看：

三、参考代码

// 登录 AlgoMooc 官网获取更多算法图解
// https://www.algomooc.com
// 作者：程序员吴师兄
// 代码有看不懂的地方一定要私聊咨询吴师兄呀
// 二叉树的最大深度（ LeetCode 104 ）: https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
class Solution {
    public int maxDepth(TreeNode root) {

        // 如果 root 为空，直接返回 0
        if(root == null) return 0;

        // 递归调用 maxDepth，求出当前节点的左子树的最大深度
        int left = maxDepth(root.left);

        // 递归调用 maxDepth，求出当前节点的右子树的最大深度
        int right = maxDepth(root.right);

        // 求出当前节点的左右子树中较大的值
        int childMaxDepth = Math.max(left,right);

        // 二叉树的最大深度就是它的左右子树中较大的值加上 1
        return childMaxDepth + 1;
    }
}