剑指 Offer 41. 数据流中的中位数

大家好，我是吴师兄。

今天继续来学习《剑指Offer》系列的一道经典题目，依旧给出了非常详细的题解和精美的配图与动画。

一、题目描述

如何得到一个数据流中的中位数？

如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。

如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。

例如，

[2,3,4] 的中位数是 3

[2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

• void addNum(int num) - 从数据流中添加一个整数到数据结构中。
• double findMedian() - 返回目前所有元素的中位数。

示例 1：

输入：["MedianFinder","addNum","addNum","findMedian","addNum","findMedian"]
[[],[1],[2],[],[3],[]]
输出：[null,null,null,1.50000,null,2.00000]

示例 2：

输入：
["MedianFinder","addNum","findMedian","addNum","findMedian"]
[[],[2],[],[3],[]]
输出：[null,null,2.00000,null,2.50000]

限制：

• 最多会对 addNum、findMedian 进行 50000 次调用。

二、题目解析

这道题目得先了解以下几个基础概念：

• 1、中位数指的是排序数组的中间元素值，如果是奇数，那么直接就是中间的数值；如果是偶数，那么就是中间两个数的平均值。

• 2、数据流指的是数据的长度是动态变化的，就像流水一样，在不断的新增数据过来。

这意味着，数据流的中位数在不断的变化，不仅值在变化，求解方式也是在动态变化。

并且，我们是需要不断的将数据流中的全部数字进行排序，那么这里就要借助堆的知识了。

设置两个堆，一个是大顶堆 maxHeap，一个是小顶堆 minHeap。

• 大顶堆 maxHeap 来存储数据流中较小一半的值
• 小顶堆 minHeap 来存储数据流中较大一半的值

由于大顶堆的堆顶为它的存储区间的最大值，小顶堆的堆顶为它的存储区间的最小值，那么如果用着两个堆来存储数据流的所有数据，我们可以组成一个递增有序的数组。

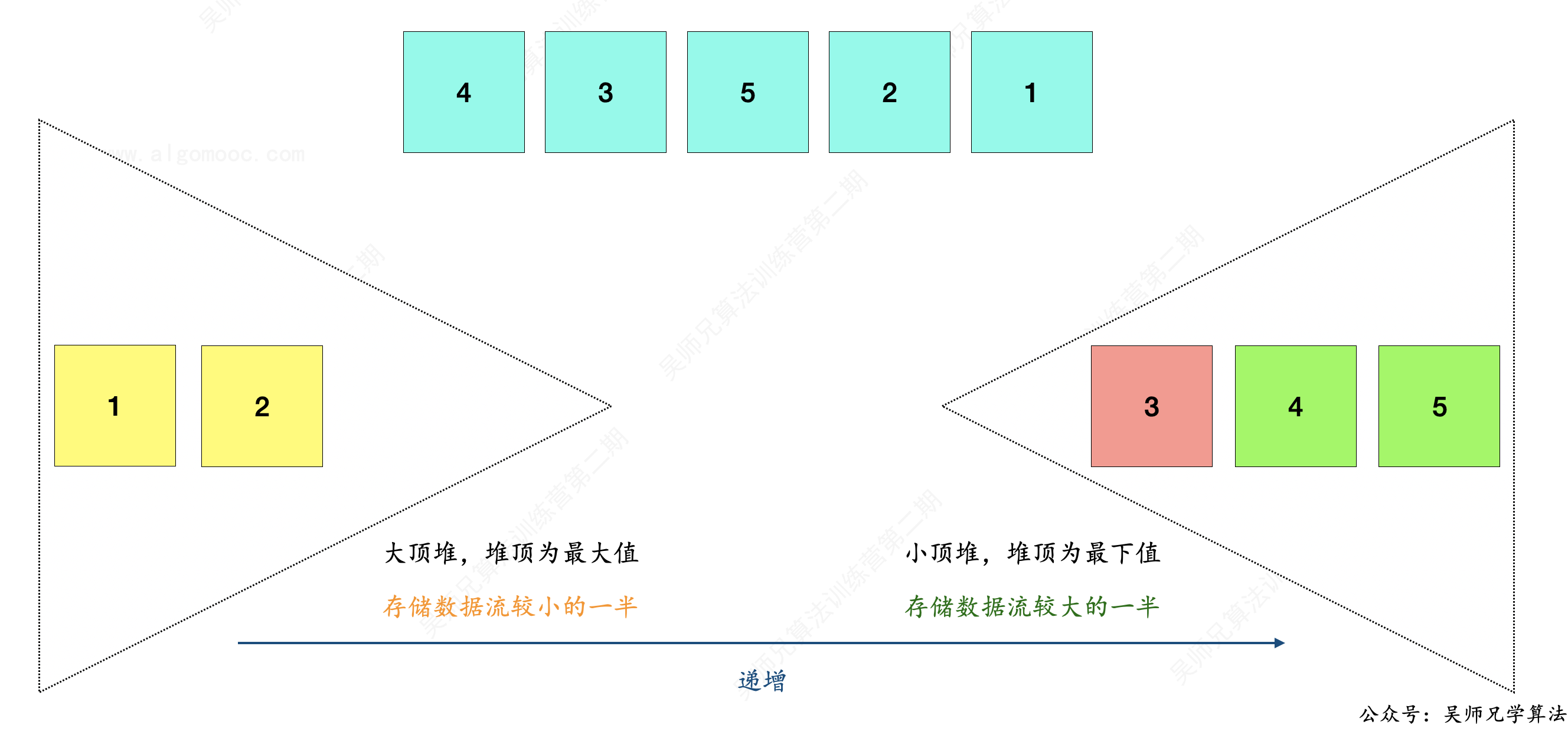
• 1、大顶堆从左到右递增
• 2、小顶堆从左到右递增

在动态存储数据流的数据过程中，中位数也就是这两种情况：

• 1、数据流为奇数时，保证两个堆的长度相差 1，小顶堆的堆顶就是中位数。
• 2、数据流为偶数时，保证两个堆的长度相等，两个堆的堆顶相加除二就是中位数。

那一个新来的数据应该添加到哪个堆呢？

• 1、当两堆长度相等，即长度都为 n 时，新数据加入到小顶堆中，使得小顶堆的长度为 n + 1，那么证两个堆的长度相差 1，小顶堆的堆顶就是中位数。
• 2、当两堆长度不相等，即小顶堆长度为 n，大顶堆长度为 n - 1，新数据加入到大顶堆中，使得大顶堆的长度为 n ，那么两个堆的长度就相等，两个堆的堆顶相加除二就是中位数。

但是，这样做会有一个问题。

比如下面这张图：

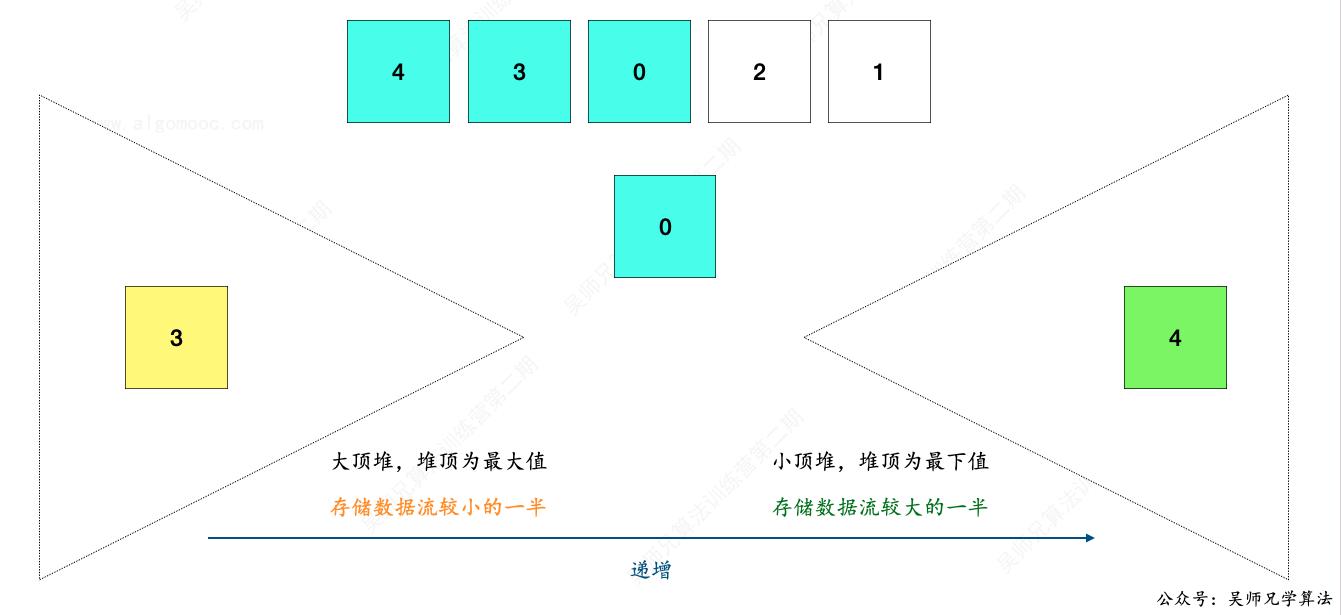
此时，两堆长度相等，即长度都为 n 时，如果直接把新数据加入到小顶堆中，使得小顶堆的长度为 n + 1，那么从大顶堆到小顶堆，并非是一个递增有序的数组了。

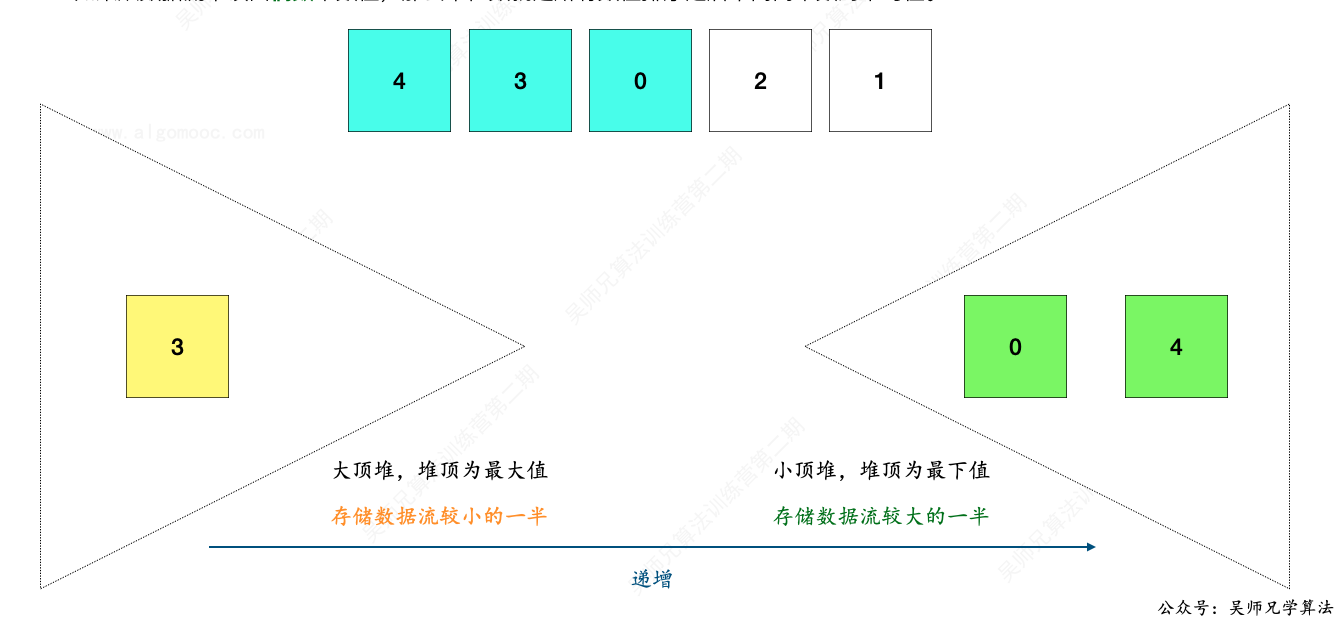
为了让每次新增一个数据到两个堆之后，都能使得从大顶堆到小顶堆是一个递增有序的数组，我们可以采取如下的操作。

1）、如果两堆长度相等，即长度都为 n 时，新数据先加入到大顶堆中，然后再把大顶堆的堆顶元素取出，放入到小顶堆中。

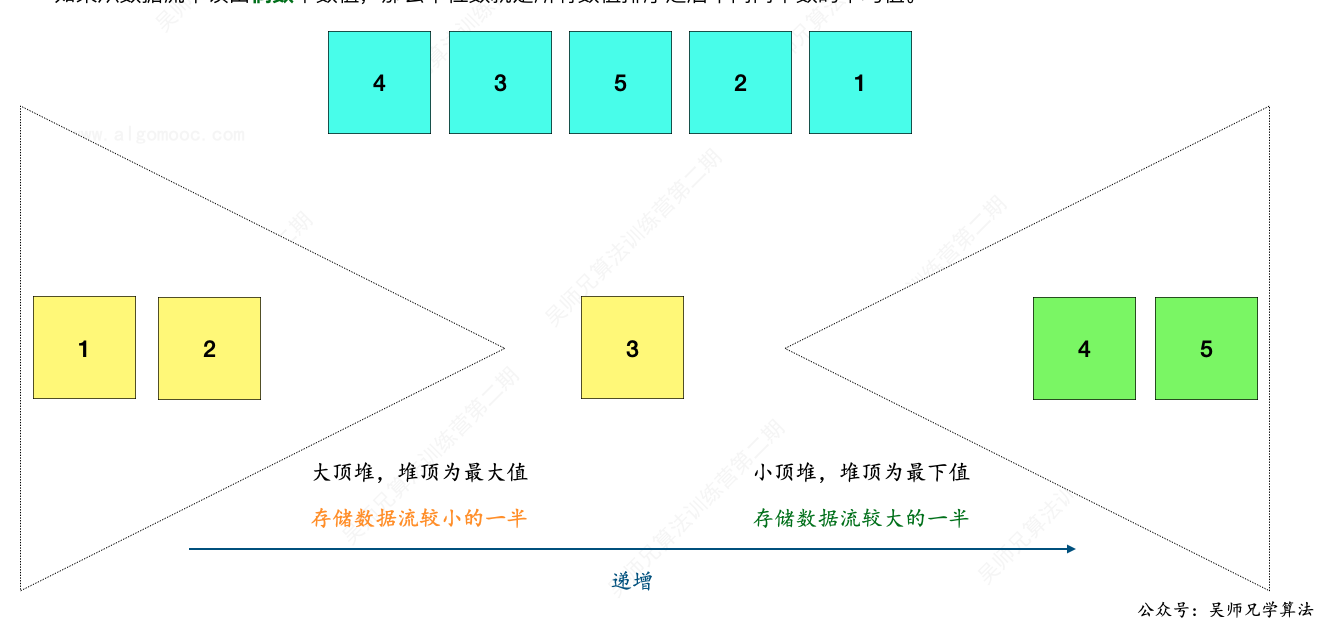
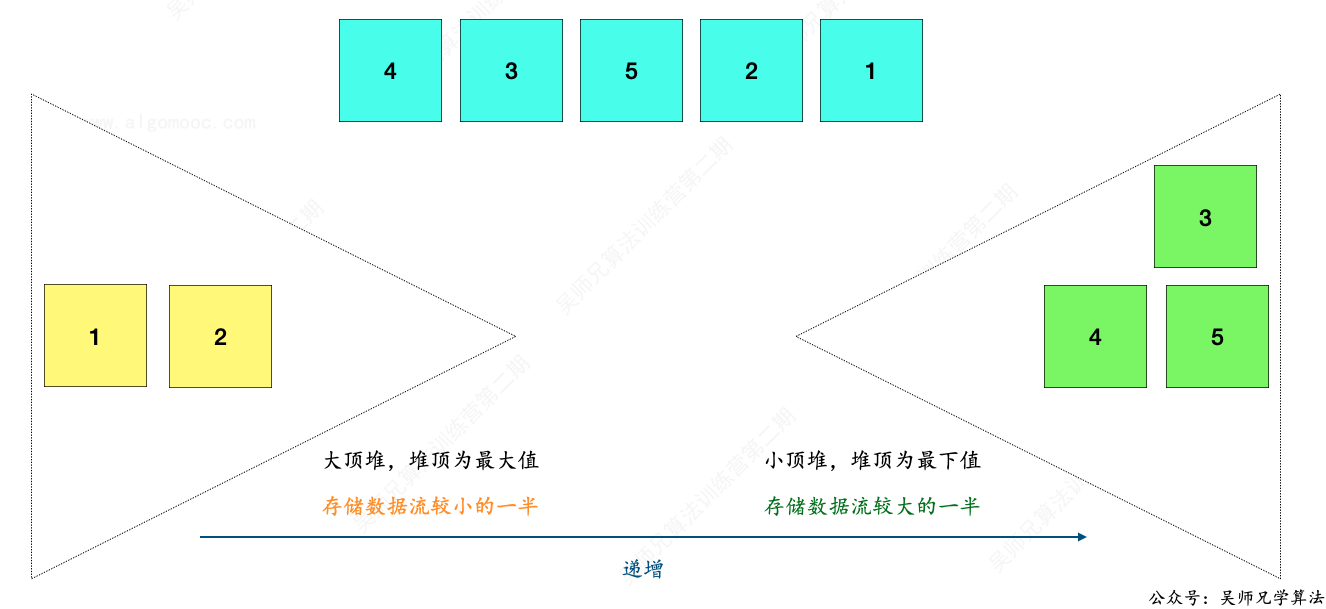
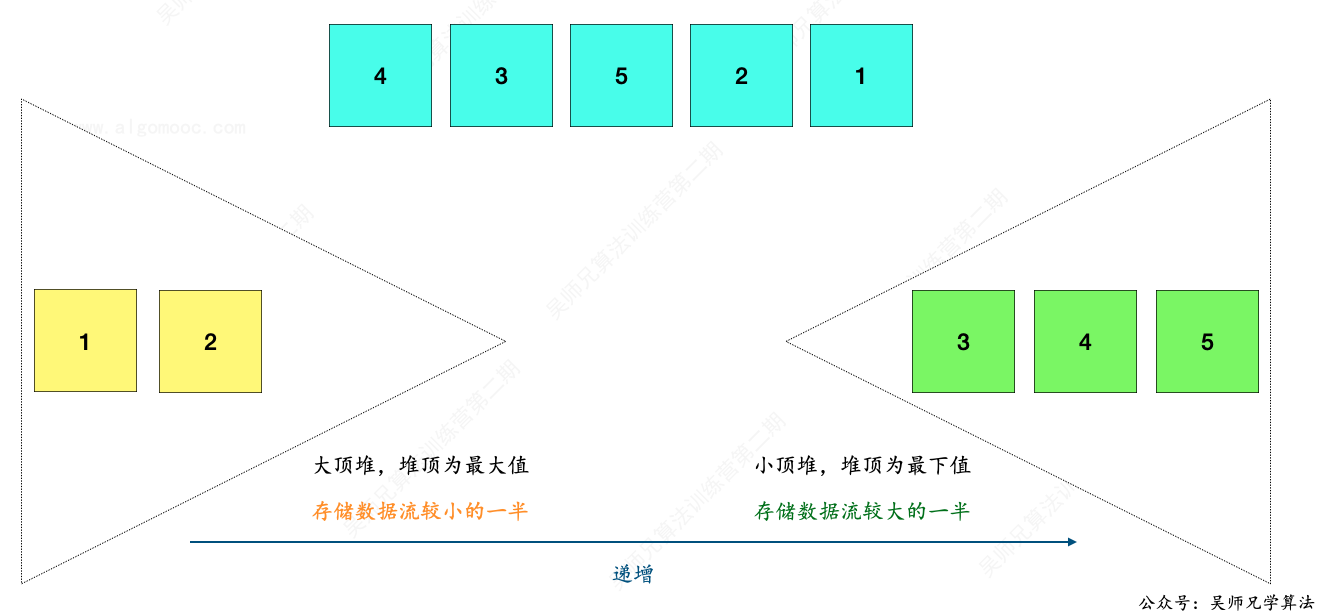
比如，大顶堆和小顶堆的长度均为 2，新增一个元素 1。

先把新数据 1 加入到大顶堆中。

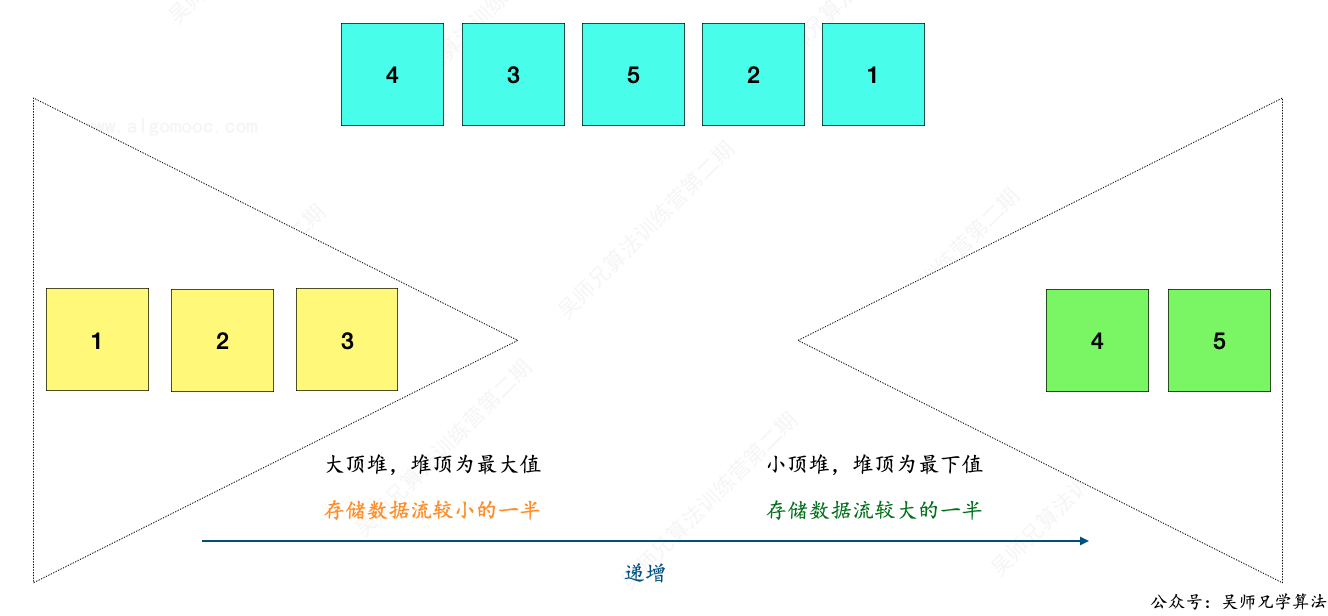
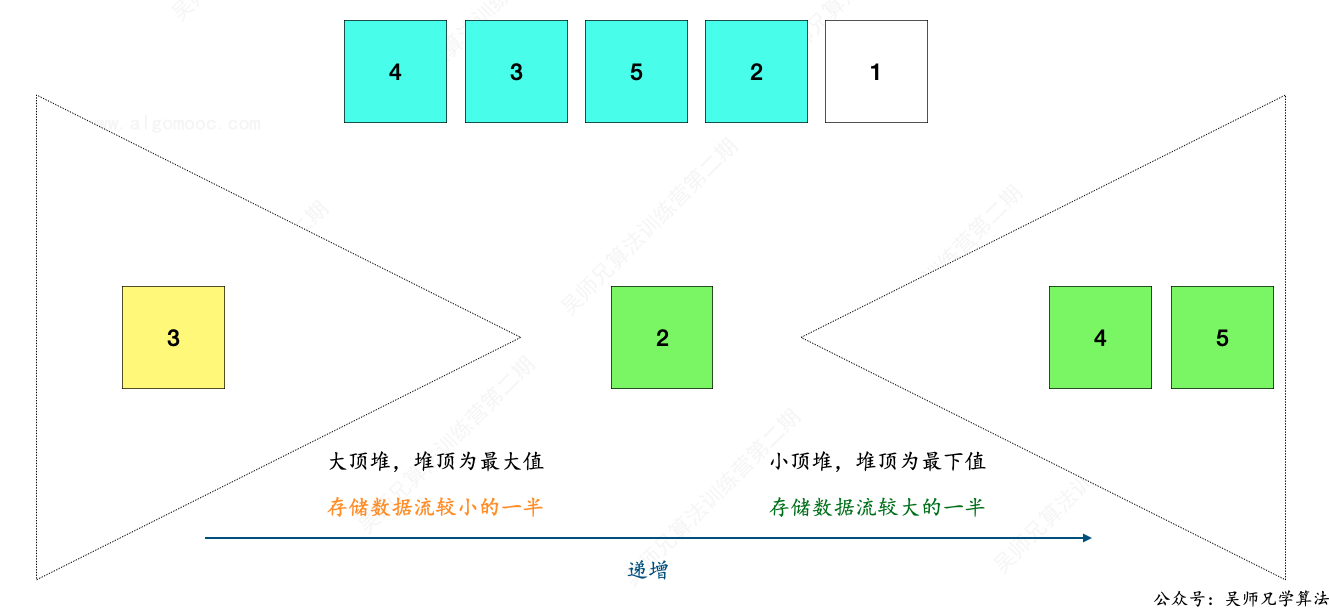
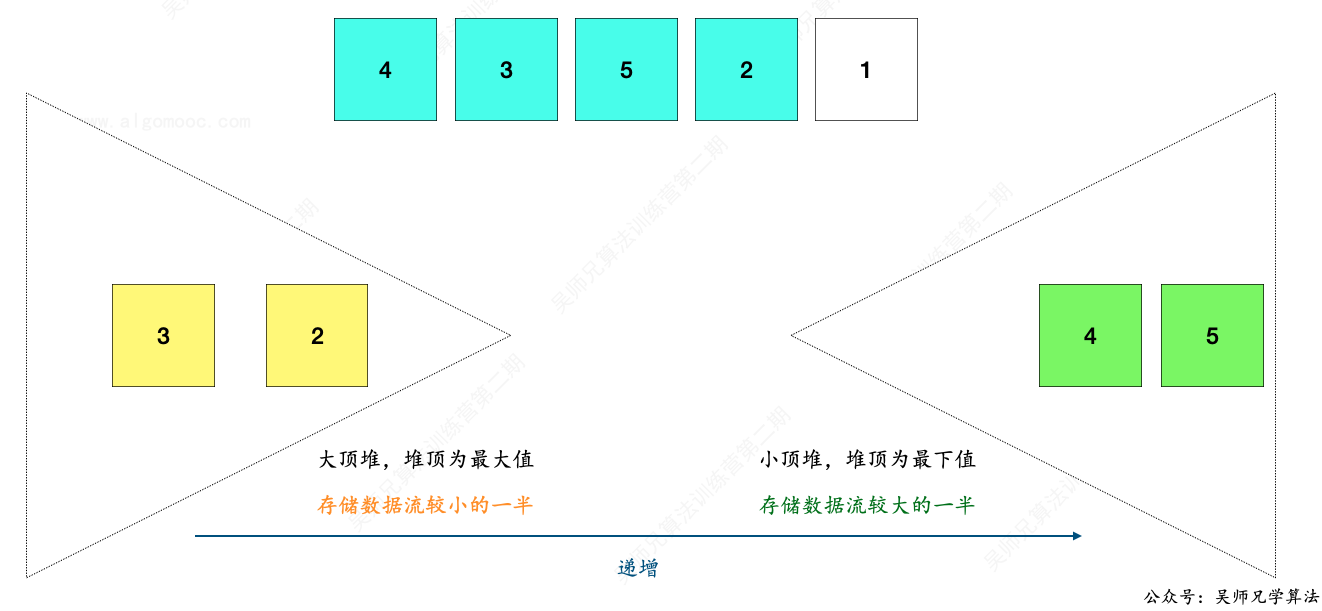
然后再把大顶堆的堆顶元素取出，放入到小顶堆中。

2）、当两堆长度不相等，即小顶堆长度为 n，大顶堆长度为 n - 1，新数据先加入到小顶堆中，然后再把小顶堆的堆顶元素取出，放入到大顶堆中。

比如，大顶堆的长度 1 ，小顶堆的长度为 2，新增一个元素 2。

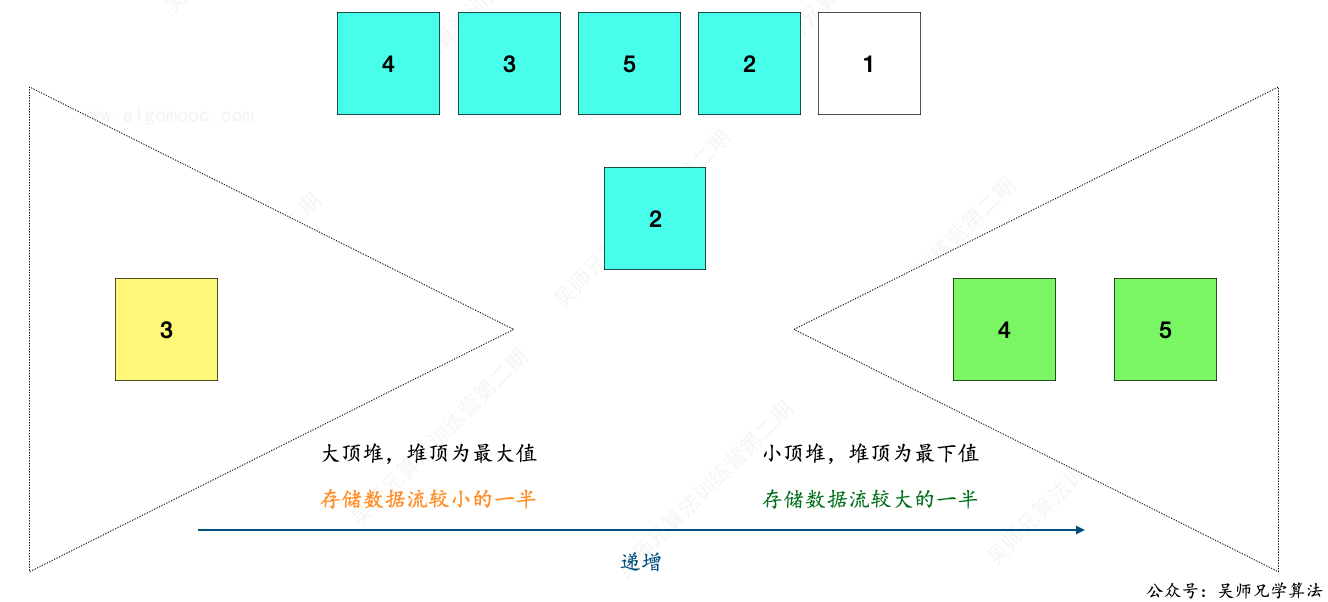
先把新数据 2 加入到小顶堆中。

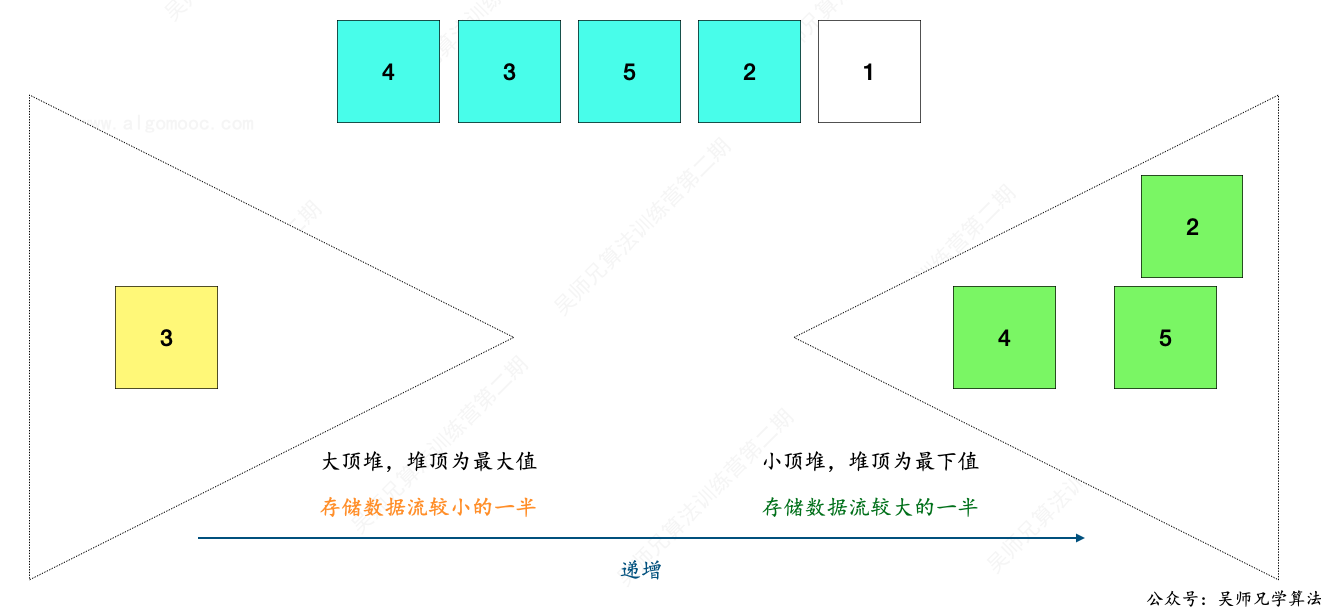
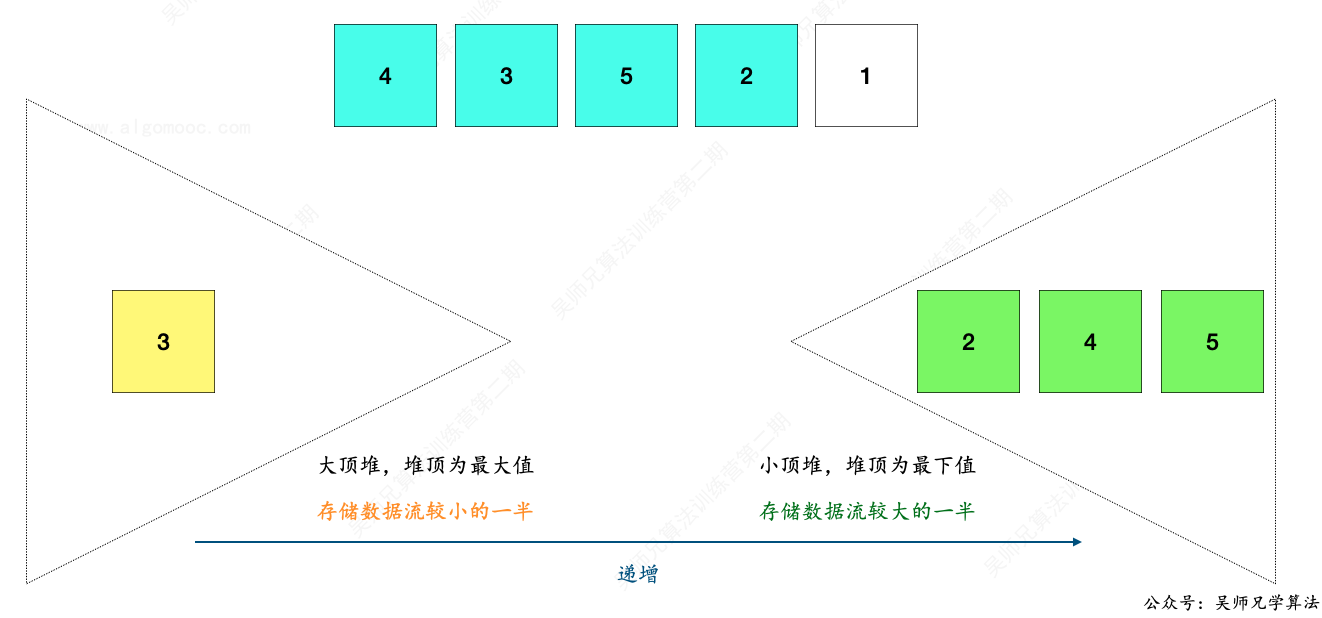
然后再把小顶堆的堆顶元素取出，放入到大顶堆中。

为了帮助你更好的理解整个过程，我特意做了一组动画，点开可以查看：

三、参考代码

// 登录 AlgoMooc 官网获取更多算法图解
// https://www.algomooc.com
// 作者：程序员吴师兄
// 代码有看不懂的地方一定要私聊咨询吴师兄呀
// 剑指 Offer 41. 数据流中的中位数:https://leetcode-cn.com/problems/shu-ju-liu-zhong-de-zhong-wei-shu-lcof/
class MedianFinder {
    
    // PriorityQueue，优先队列
    // 优先队列的作用是能保证每次取出的元素都是队列中权值最小的（ Java 的优先队列每次取最小元素，C++的优先队列每次取最大元素）
    // 由于 Java 的优先队列每次取最小元素，即默认函数是实现小顶堆
    // 大顶堆的概念：每个节点的值大于等于左右孩子节点的值，堆顶为最大值
    // 因此，大顶堆的初始化需要额外处理
    // maxHeap 存储数据流中较小一半的值
    PriorityQueue<Integer> maxHeap;
    
    // 小顶堆的概念：每个节点的值小于等于左右孩子节点的值，堆顶为最小值
    // minHeap 来存储数据流中较大一半的值
    PriorityQueue<Integer> minHeap;

    public MedianFinder() {

        // 初始化操作
        maxHeap = new PriorityQueue<Integer>((x, y) -> (y - x));

        minHeap = new PriorityQueue<Integer>();
    }
    
    // 根据我们的设定，一直维护大顶堆、小顶堆的特性
    // 使得 maxHeap堆底 <= maxHeap堆顶 <= minHeap堆顶 <= minHeap堆底
    // 那么，中位数就是在【大顶堆的堆顶】与【小顶堆的堆顶】中间的位置
    // 在添加元素的过程中，需要判断添加的元素应该添加到哪个堆中
    // 小的值应该插入到 maxHeap，大的值应该插入到 minHeap
    
    public void addNum(int num) {

        // 数据流的长度有奇数和偶数两种情况，并且是在动态变化的

        // 1、【大顶堆】与【小顶堆】的长度不相等，由于两者的长度至多相差 1，那么数据流的总长度就是奇数
        // 假设 minHeap 的长度为 n，则 maxHeap 的长度为 n - 1
        // 那么 maxHeap 是应该需要加入一个【新的元素】的，这样就能使得 minHeap 和 maxHeap 的长度均为 n
        // 那么加入新元素之后，中位数就是 （ minHeap 的堆顶 + maxHeap 的堆顶） / 2
        // 但如果直接把 num 加入到 maxHeap 中，如果 num 是一个很大的值
        // 由于 maxHeap 是存储数据流中较小一半的值，这样就会破坏我们维护的属性
        // 因此，我们可以先把 num 加入到 minHeap 中，然后从 minHeap 挤出一个最小值来，重新加入到 maxHeap
        // 一来一回，minHeap 的长度依旧为 n，maxHeap 的长度变成了 n
        if(maxHeap.size() != minHeap.size()) {

            // 先将元素添加到小顶堆 minHeap 中
            // 由于 minHeap 添加了新的元素，PriorityQueue 会自动的将 minHeap 之前的元素和 num 进行操作
            // 使得 minHeap 的每个节点的值小于等于左右孩子节点的值，堆顶为最小值
            // 这个时候，minHeap 的长度变成了 n + 1
            minHeap.add(num);

            // 由于 minHeap 来存储数据流中较大一半的值，而新添加的元素 num 有可能是一个很小的值
            // 理论上应该要加入到 maxHeap 才对
            // 所以，先去获取此时 minHeap 的堆顶元素（不一定值是 num），即最小值，把它抛出后加入到 maxHeap 中
            maxHeap.add(minHeap.poll());



        // 2、【大顶堆】与【小顶堆】的长度相等，那么数据流的总长度就是偶数
        // 假设 minHeap 的长度为 n，则 maxHeap 的长度为 n 
        // 我们把新的元素加入到 minHeap 中，使得 minHeap 的长度变成了 n + 1
        // 那么中位数就是 minHeap 的堆顶元素了
        // 但如果直接把 num 加入到 minHeap 中，如果 num 是一个很小的值
        // 由于 minHeap 是存储数据流中较大一半的值，这样就会破坏我们维护的属性
        // 因此，我们可以先把 num 加入到 maxHeap 中，然后从 maxHeap 挤出一个最大值来，重新加入到 minHeap
        // 一来一回，maxHeap 的长度依旧为 n，mminHeap 的长度变成了 n + 1
        } else {
            
            // 先将元素添加到大顶堆 maxHeap 中
            // 由于 maxHeap 添加了新的元素，PriorityQueue 会自动的将 maxHeap 之前的元素和 num 进行操作
            // 使得 maxHeap 的每个节点的值大于等于左右孩子节点的值，堆顶为最大值
            // 这个时候，maxHeap 的长度变成了 n + 1
            maxHeap.add(num);
            
            // 由于 maxHeap 来存储数据流中较小一半的值，而新添加的元素 num 有可能是一个很大的值
            // 理论上应该要加入到 minHeap 才对
            // 所以，先去获取此时 maxHeap 的堆顶元素（不一定值是 num），即最大值，把它抛出后加入到 minHeap 中
            minHeap.add(maxHeap.poll());

        }
    }
    
    public double findMedian() {

        // 数据流的长度有奇数和偶数两种情况，并且是在动态变化的
        
        // 1、【大顶堆】与【小顶堆】的长度不相等，由于两者的长度至多相差 1，那么数据流的总长度就是奇数
        // 假设 minHeap 的长度为 n，则 maxHeap 的长度为 n - 1
        // 那么中位数出现在 minHeap 的堆顶位置
        if(maxHeap.size() != minHeap.size()) {
            return minHeap.peek();

        // 2、【大顶堆】与【小顶堆】的长度相等，那么数据流的总长度就是偶数
        // 假设 minHeap 的长度为 n，则 maxHeap 的长度为 n 
        // 那么中位数就是 （ minHeap 的堆顶 + maxHeap 的堆顶） / 2
        } else {
            return (maxHeap.peek() + minHeap.peek()) / 2.0;
        }
    }
}