# 剑指 Offer 33. 二叉搜索树的后序遍历序列
大家好,我是吴师兄。
今天继续来学习《剑指Offer》系列的一道经典题目,依旧给出了非常详细的题解和精美的配图与动画。
# 一、题目描述
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
5
/ \
2 6
/ \
1 3
示例 1:
输入: [1,6,3,2,5]
输出: false
示例 2:
输入: [1,3,2,6,5]
输出: true
提示:
数组长度 <= 1000
# 二、题目解析
这道题目首先得掌握以下基础概念:
- 1、二叉搜索树
- 2、后序遍历的递归写法
二叉搜索树是一棵有序的二叉树,它具有如下的性质:
- 1、若它的左子树不为空,那么左子树上的所有值均小于它的根节点
- 2、若它的右子树不为空,那么右子树上所有值均大于它的根节点
- 3、它的左子树和右子树也都是二叉搜索树
而后序遍历的递归过程是 左 ---》右 ---》根 的顺序。
比如对于下面这棵二叉搜索树来说,它的后序遍历序列是 [4, 8, 6, 12, 16, 14, 10]。
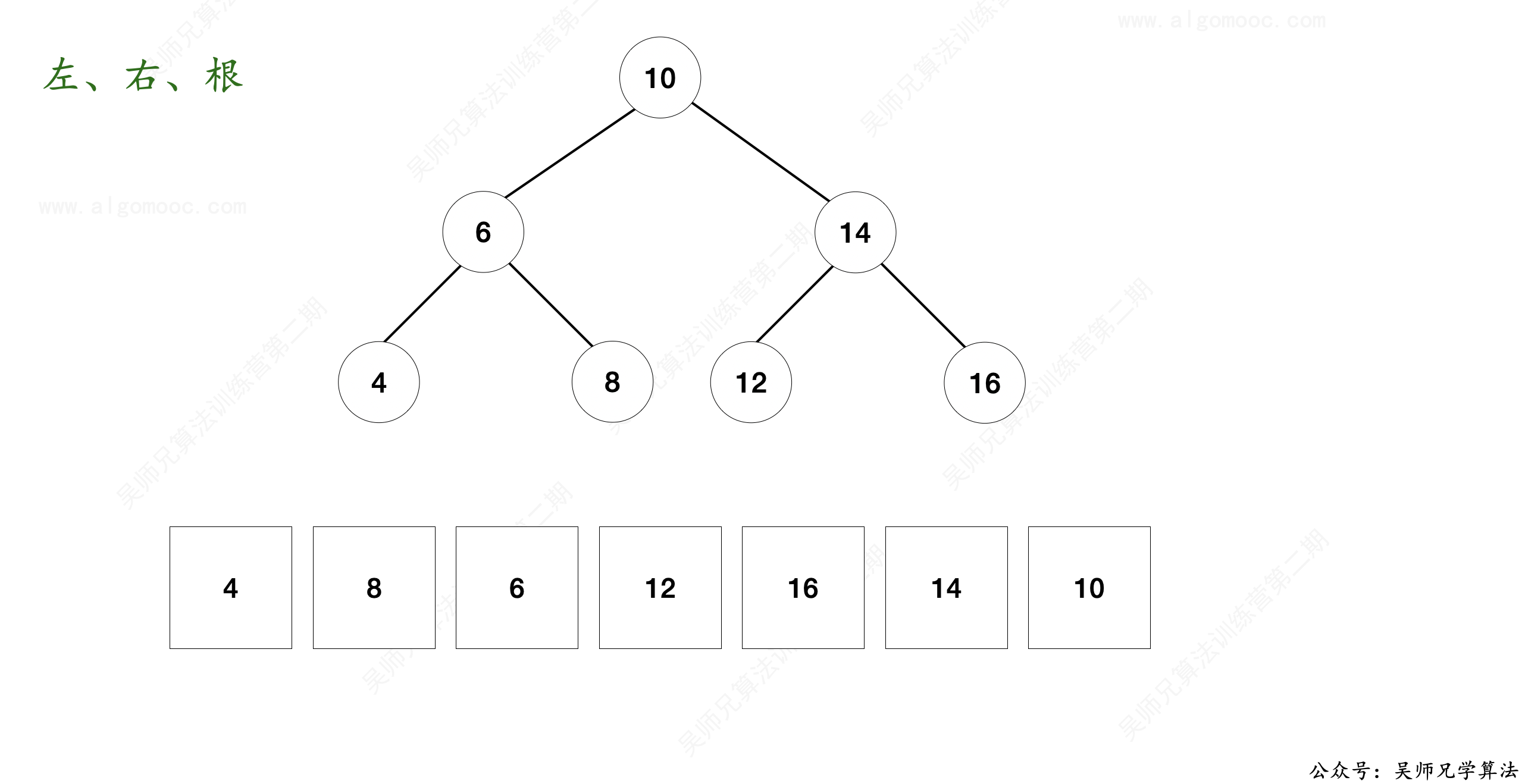
由于后序遍历的过程中是不断的执行 左 ---》右 ---》根 的顺序,那也就意味着结果数组的最后一个数字必然是二叉搜索树的根节点。
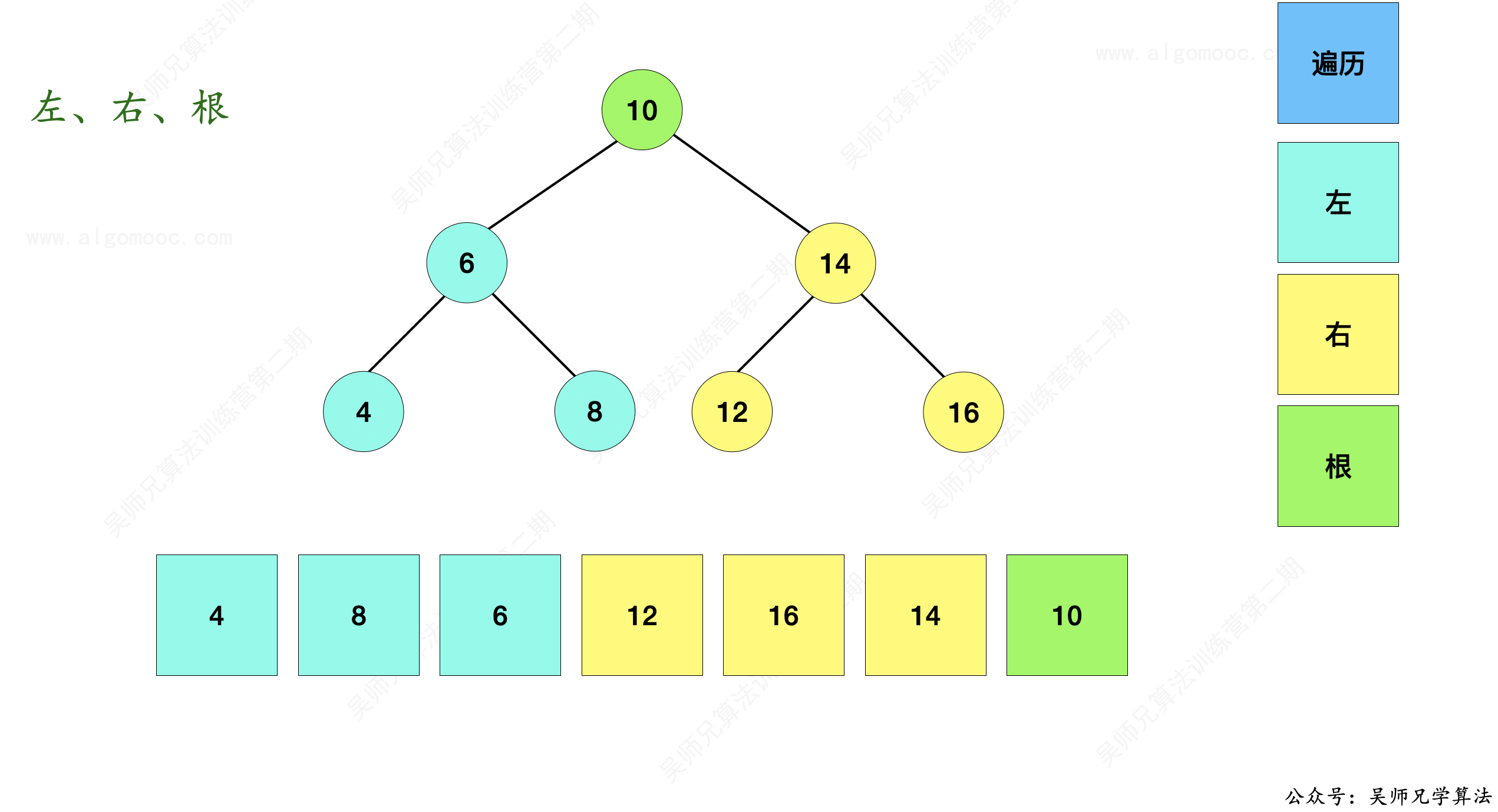
如果这个数组是二叉搜索树的后序遍历结果,那么在这个根节点 10 的前面既有它的左子树又有它的右子树,并且左右子树是扎堆出现的,即小于 10 的那些节点是连续排列的,大于 10 的那些节点也是连续排列的。
因此,我们可以从头到尾去遍历 10 前面的数字,找到第一个大于 10 的位置,这个位置前面的数都小于了 10 ,是它的左子树,这个位置后面的数都大于了 10,是它的右子树。
也就是如上图所示,划分为了青、黄、绿三个区域。
只要在黄色区域里面发现了小于 10 的值,那么就知道它不是二叉搜索树了。
比如后序遍历序列 [4, 8, 6, 12, 16, 9, 10]。
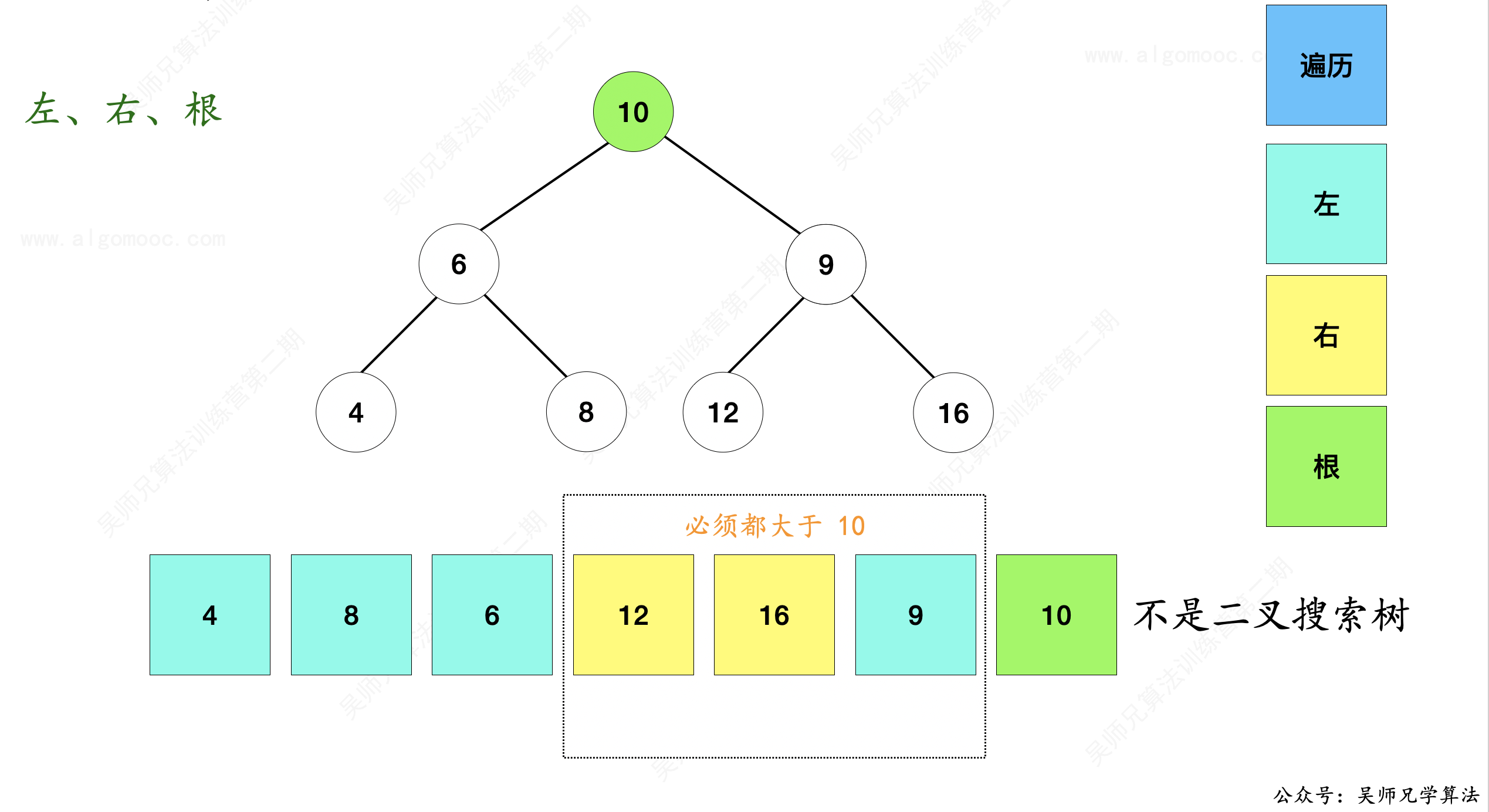
12 前面的都小于了 10 ,是 10 的左子树,12 后面的数字都是 10 的右子树,但对于二叉搜索树来说,右子树所有的节点都应该大于根节点的值,而 9 < 10 ,因此这棵二叉树不是二叉搜索树。
接下来,我们来看一下完整的操作:
1、获取数组最后一个节点的值,它是树的根节点,此时节点值为 10。
2、从头到尾遍历数组,直到遍历到第一个大于根节点 10 的值为止。
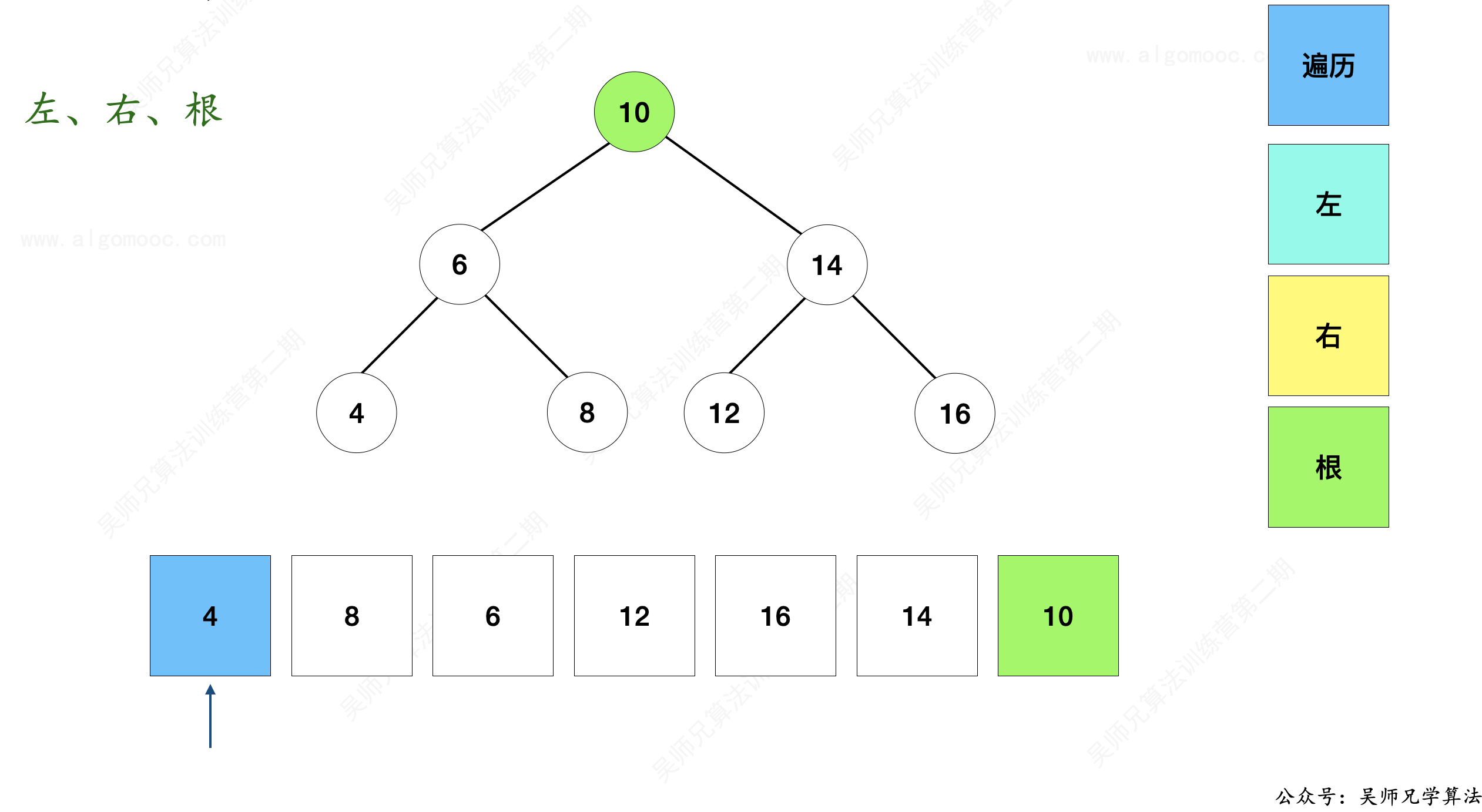
3、遍历过程中,发现 12 这个节点是第一个大于根节点 10 的值。
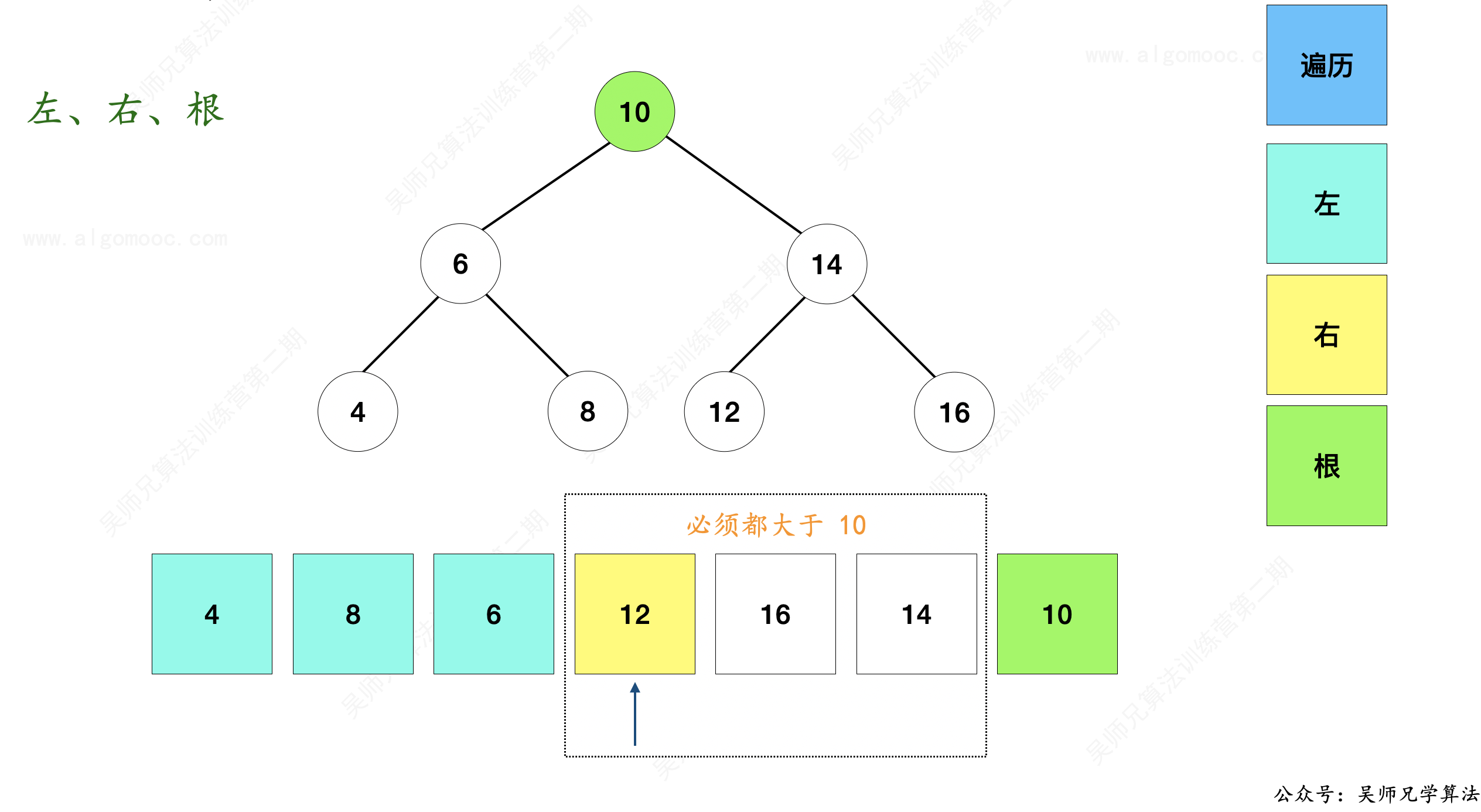
4、如果它是一棵二叉搜索树,那么从 12 开始,后面所有的节点值都应该大于 10,如果出现一个小于 10 的值,那么就不是二叉搜索树,直接返回 false 就行,否则,整个数组就被划分为三个区域。
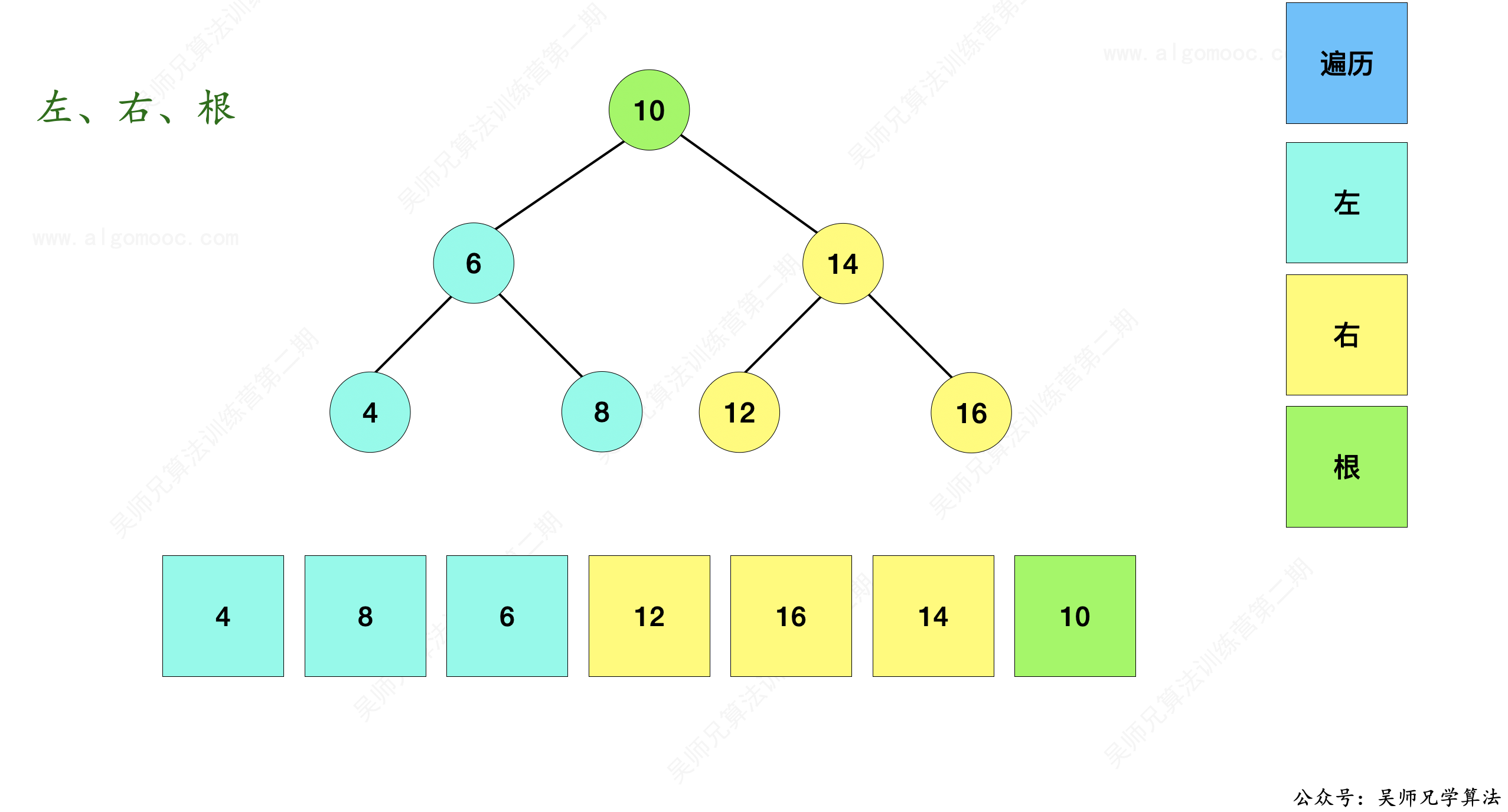
5、接下来,依次递归的判断左子树(青色区域)、右子树(黄色区域)是否也是二叉搜索树。
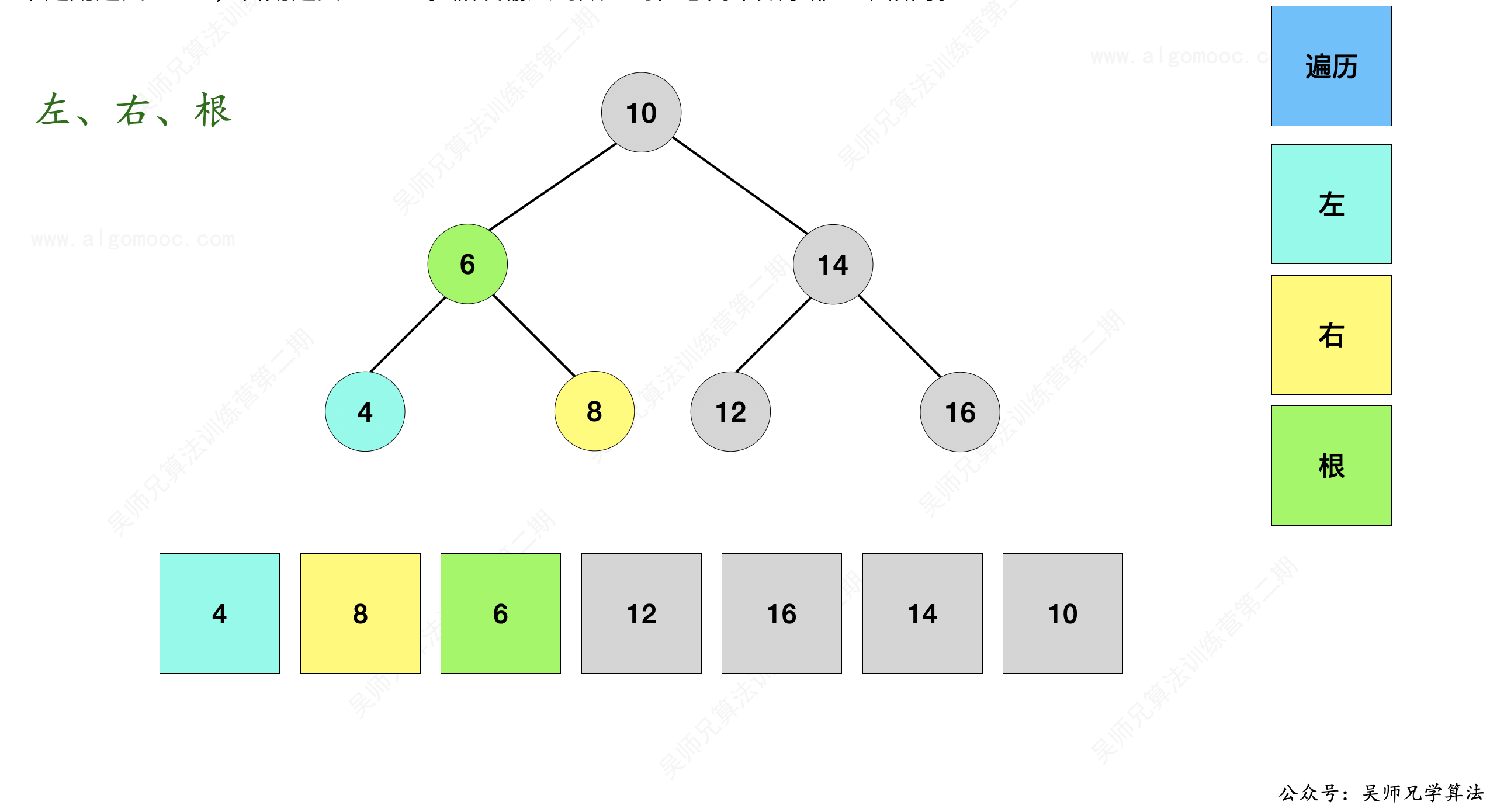
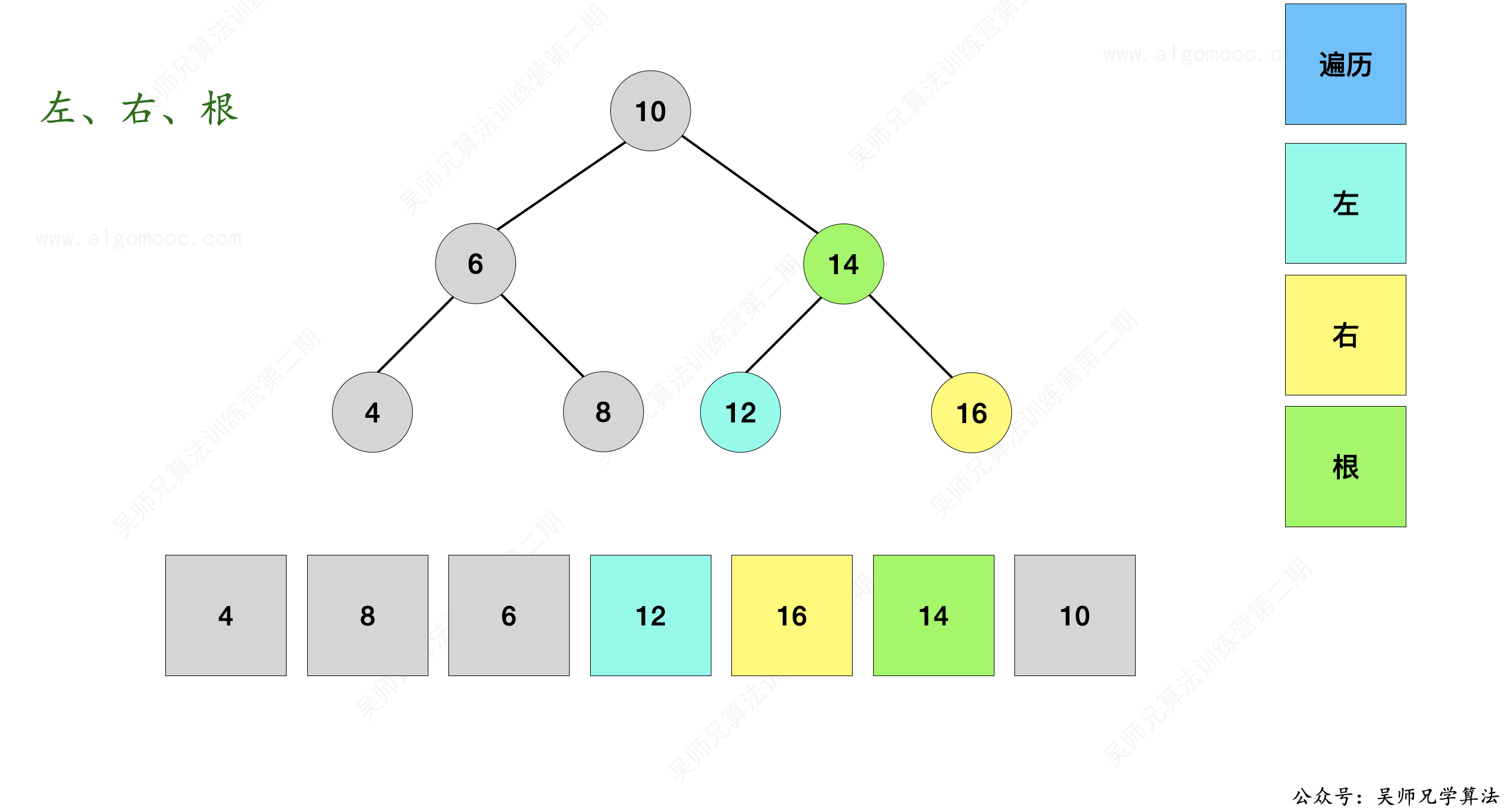
为了帮助你更好的理解整个过程,我特意做了一组动画,点开可以查看:
#
# 三、参考代码
// 登录 AlgoMooc 官网获取更多算法图解
// https://www.algomooc.com
// 作者:程序员吴师兄
// 代码有看不懂的地方一定要私聊咨询吴师兄呀
// 剑指 Offer 33. 二叉搜索树的后序遍历序列:https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-hou-xu-bian-li-xu-lie-lcof/
class Solution {
public boolean verifyPostorder(int[] postorder) {
// 递归的调用 isPostorder ,判断任意一棵子树是否是二叉搜索树
return isPostorder( postorder , 0 , postorder.length - 1);
}
private boolean isPostorder(int[] postorder , int left , int right ){
// 当 left >= right 时,说明当前区间只有一个节点或者没有节点了
// 不需要在判断下去
if( left >= right) return true;
// 先去后去当前区间最后一个节点的值
// 由于是后序遍历,即采取 左、右、根的顺序遍历
// 那么这个节点实际上是根节点
int rootNodeValue = postorder[right];
// 接下来,需要在这个区间里找出 rootNode 的左子树与右子树
int firstRightNodeIndex = left;
// 从左到右遍历当前区间,找到第一个大于 rootNodeValue 的位置
// 这个位置前面的数都小于了 rootNodeValue ,是它的左子树
// 这个位置后面的数都大于了 rootNodeValue ,是它的右子树
while( postorder[firstRightNodeIndex] < rootNodeValue ){
firstRightNodeIndex += 1;
}
// 接下来判断从 firstRightNodeIndex 到 right 这个区间中,是否存在比 rootNodeValue 更小的值
int curNodeIndex = firstRightNodeIndex;
while( curNodeIndex < right){
curNodeIndex += 1;
// 如果发现从 firstRightNodeIndex 到 right 这个区间中存在比 rootNodeValue 更小的值
// 根据二叉搜索树的性质,它的右子树的所有节点都必须大于根节点
// 此时,不符合这个性质,意味着这不是一棵二叉搜索树
if( postorder[curNodeIndex] < rootNodeValue ){
return false;
}
}
// 当代码执行到这里的时候,rootNode 的左子树值都小于了 rootNodeValue
// rootNode 的右子树值都大于了 rootNodeValue
// 接下来,递归的判断它的左子树、右子树是否是二叉搜索树
return isPostorder( postorder , left , firstRightNodeIndex - 1 )
&&
isPostorder( postorder , firstRightNodeIndex , right - 1);
}
}