剑指 Offer 51. 数组中的逆序对

大家好，我是吴师兄。

今天继续来学习《剑指Offer》系列的一道经典题目，依旧给出了非常详细的题解和精美的配图与动画。

一、题目描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

输入: [7,5,6,4]
输出: 5

限制：

0 <= 数组长度 <= 50000

二、题目解析

这道题目首先得掌握归并排序的基础知识。

1、分解（Divide）：将 n 个元素分成个含 n / 2 个元素的子序列。

2、解决（Conquer）：用合并排序法对两个子序列递归的排序。

3、合并（Combine）：合并两个已排序的子序列已得到排序结果。

而在第二步解决的过程中，不断的通过比较的方式合并两个排序数组，在这个操作中，如果遇到 左子数组当前元素 > 右子数组当前元素，意味着 「左子数组当前元素 至 末尾元素」 与 「右子数组当前元素」 构成了若干 「逆序对」 。

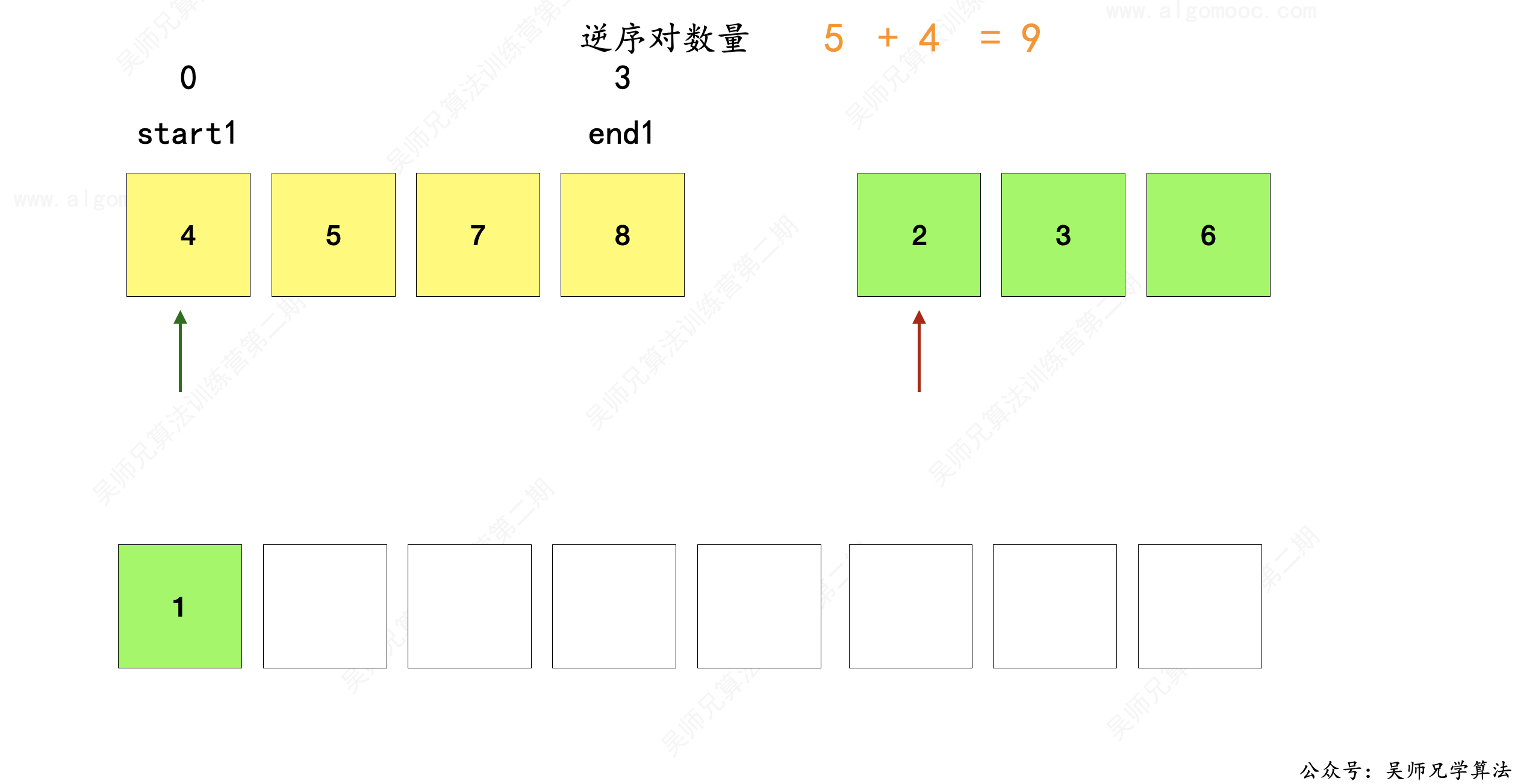
比如 4 与 2 进行比较，4 > 2，它们是一组逆序对，又因为黄色区域从左到右是递增的，那也就意味着从 start1 到 end1 所有的元素都大于了 2，都和 2 构成了逆序对。

所以，我们只需要在归并排序的代码上添加一行统计逆序对的代码就行。

为了帮助你更好的理解整个过程，我特意做了一组动画，点开可以查看：

三、参考代码

// 登录 AlgoMooc 官网获取更多算法图解
// https://www.algomooc.com
// 作者：程序员吴师兄
// 代码有看不懂的地方一定要私聊咨询吴师兄呀
// 剑指 Offer 51. 数组中的逆序对： https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof/solution/
class Solution {

    // 记录逆序对的数量
    private int count;

    public int reversePairs(int[] nums) {

        // 初始化为 0
        count = 0 ;

        int[] result = new int[nums.length];

        // 通过归并排序的方式，不断的记录逆序对的数量
        merge_sort_recursive(nums,result,0,nums.length - 1);

        return count;

    }

    public void merge_sort_recursive(int[] arr, int[] result, int start, int end) {

        // 1、分解到最小需要解决的地步，无法再分解了
        if (start >= end){
            // 需要开始解决问题
            return;
        }

        // 2、解决

        // 计算数组 arr 的中间位置    
        int mid = (start + end ) / 2;

        // start1 为左区间的开始位置
        int start1 = start;

        // end1 为左区间的结束位置
        int end1 = mid;

        // start2 为右区间的开始位置
        int start2 = mid + 1;

        // end2 为右区间的结束位置
        int end2 = end;

        // 调用 merge_sort_recursive 函数，将 arr 数组中的 start1 到 end1 这一区间的数字排序后，并存放到 result 中
        merge_sort_recursive(arr, result, start1, end1);

        // 调用 merge_sort_recursive 函数，将 arr 数组中的 start2 到 end2 这一区间的数字排序后，并存放到 result 中
        merge_sort_recursive(arr, result, start2, end2);

        // 3、合并

        // 将左右区间中较小的数字存放到 result 中，从 k 开始
        int k = start;

        while (start1 <= end1 && start2 <= end2){
            // 如果 arr[start1] < arr[start2])
            if(arr[start1] <= arr[start2]){
                // result[k] 存放的是 arr[start1]
                result[k] = arr[start1] ;
                start1++;
                k++;
            }else{
                // 否则，result[k] 存放的是 arr[start2]
                result[k] = arr[start2] ;

                // 在这里统计逆序对
                count += (end1 - start1 + 1);

                start2++;

                k++;
            }

        }

        // 如果左区间中还有元素，那么把它都添加到 result 中
        while (start1 <= end1){
            result[k] = arr[start1];
            k++;
            start1++;
        }

        // 如果右区间中还有元素，那么把它都添加到 result 中
        while (start2 <= end2){
            result[k] = arr[start2];
            k++;
            start2++;
        }

        // 最后，把结果赋值到 arr 中
        for (k = start; k <= end; k++)
            arr[k] = result[k];
    }
    
}