剑指 Offer 45. 把数组排成最小的数

大家好，我是吴师兄。

今天继续来学习《剑指Offer》系列的一道经典题目，依旧给出了非常详细的题解和精美的配图与动画。

一、题目描述

输入一个非负整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。

示例 1:

输入: [10,2]
输出: "102"

示例 2:

输入: [3,30,34,5,9]
输出: "3033459"

提示:

• 0 < nums.length <= 100

说明:

• 输出结果可能非常大，所以你需要返回一个字符串而不是整数
• 拼接起来的数字可能会有前导 0，最后结果不需要去掉前导 0

二、题目解析

题目要求把数组中所有的数字一起拼凑出一个最小的数字，我们先来看几个例子，它们是如何得到那个最小的结果的。

首先来看示例 1 ：

输入: [10,2]

对于 10 和 2 这两数来说，拼接的方式就两种：

• 1、“ 10 ” + “ 2 ” = “ 102 ”
• 2、“ 2 ” + “ 10 ” = “ 210 ”

102 是小于 210 的，也就意味着拼接过程中 10 应该放到 2 的前面。

那么，更一般的，对于两个数字 m 和 n ，拼接的方式就两种：

• 1、“ m ” + “ n ” = “ mn ”
• 2、“ n ” + “ m ” = “ nm ”

最终，我们选取哪种方式取决于 mn 和 nm 的比较。

• 1、当 mn < nm 时，选取 mn
• 2、当 nm < mn 时，选取 nm

当理解清楚了上面的概念之后，再来看一个示例：

输入: [3,30,34,1,9]

一开始 m = 3 ，n = 30，那么组成的字符串就是 “ 330 ”，如果将 m 和 n 交换一下，变成了 “303”，显然后者更小，意味着一开始 3 在前面 30 在后面这种方式是不对的，应该处理一下，让 30 放到前面而 3 放到后面。

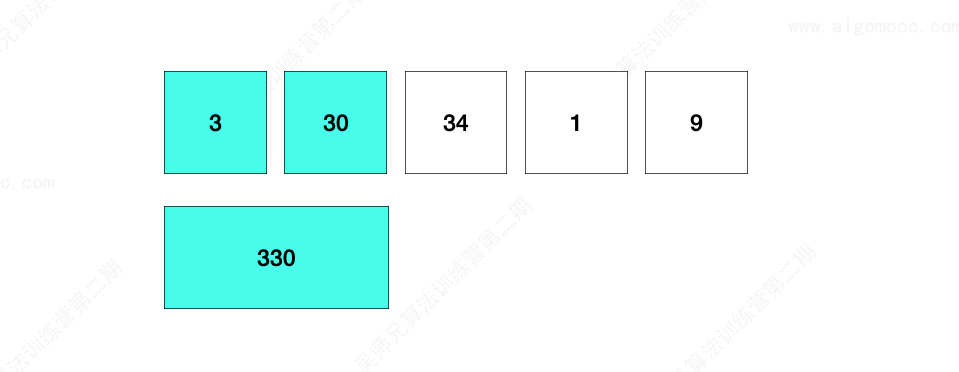
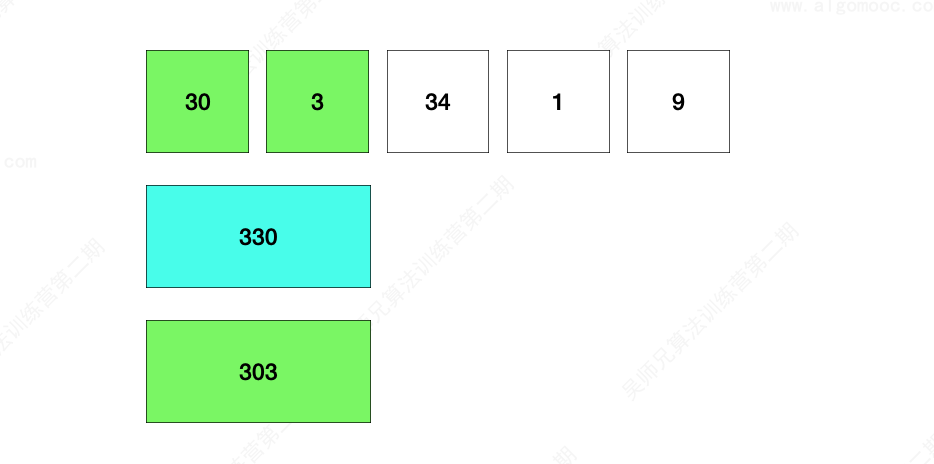
这里，我们提到了 前面 和 后面 这个两个概念，那么肯定是要有中间部分的，这样才能区分前面、后面。

由此可以进一步的联想到，最终得到的那个最小的数字必然是可以划分为三个区域：左（前面）、中、右（后面）。

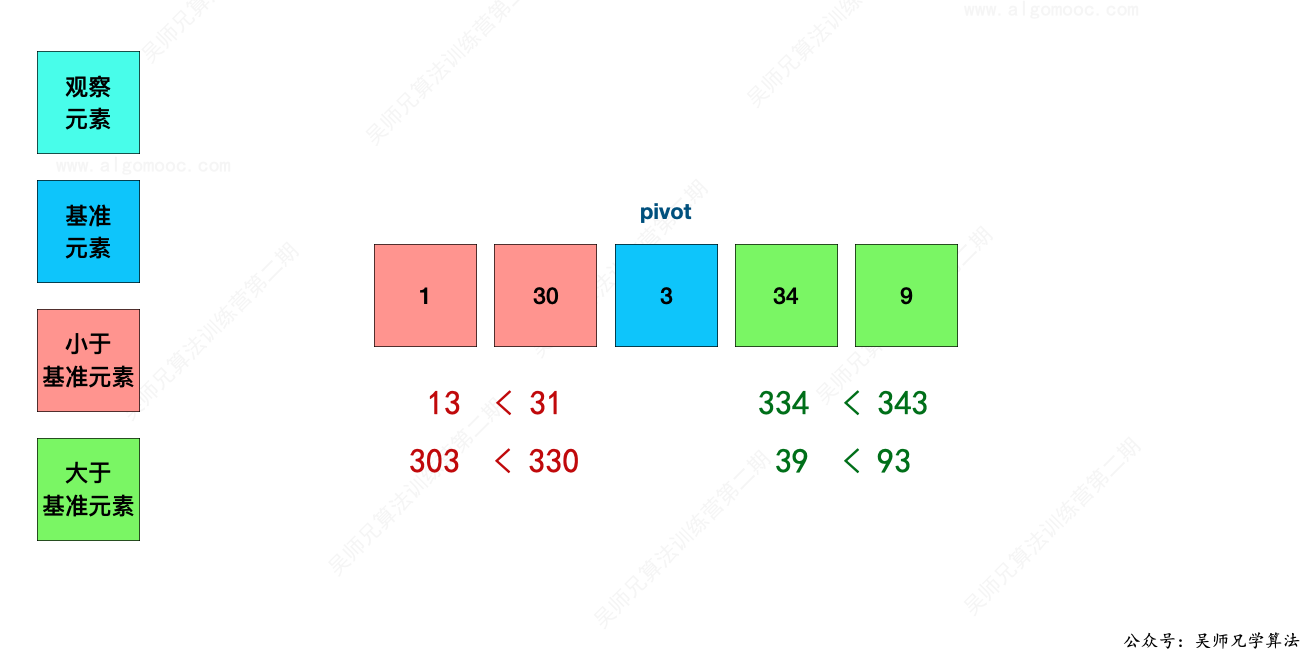
如上图所示，“ 1303349 ” 就是我们上述示例得到的最小数字，我们把红色看成左侧区域、蓝色看成中间区域、绿色看成右侧区域，这样划分之后具备如下的特征：

1、红色区域的任意数字和蓝色区域的任意数字进行拼接，都是会小于蓝色区域的任意数字和红色区域的任意数字进行拼接。

比如 1 和 3 拼接的结果小于了 3 和 1 拼接的结果。

比如 30 和 3 拼接的结果小于了 3 和 30 拼接的结果。

2、蓝色区域的任意数字和绿色区域的任意数字进行拼接，都是会小于绿色区域的任意数字和蓝色区域的任意数字进行拼接。

比如 3 和 34 拼接的结果小于了 34 和 3 拼接的结果。

比如 3 和 9 拼接的结果小于了 9 和 3 拼接的结果。

这就意味着，我们在寻找最小数字的过程中，实际上是在确定这三个区域的过程，而对于每个区域又同样可以不断的划分为左、中、右这个三个区域。

想到这个方向，实际上快速排序的概念应该能想到了，那我们来看一下是如果借助快速排序的方式解决这道题目的，具体操作如下：

1、题目说明输出结果可能非常大，需要返回一个字符串而不是整数，那么第一步就先把整型数组转换为字符串数组。

2、接下来开始对这个字符串数组进行排序操作。

3、选取第一个元素作为基准值，以这个基准值作为基础，先把字符串数组划分为三个部分：

• 左边的部分和基准值进行拼接的字符串会小于基准值和左边的部分进行拼接的字符串
• 基准值和右边的部分进行拼接的字符串会小于右边的部分和基准值进行拼接的字符串

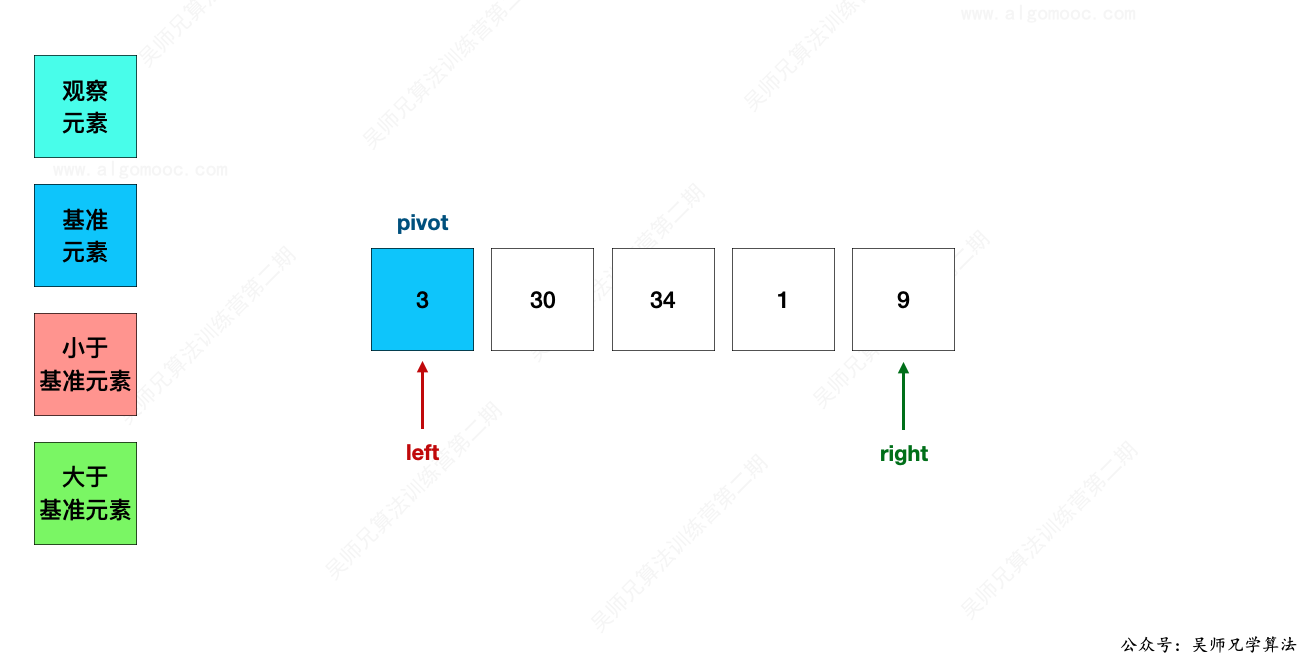
先来看右边部分的 9 这个数字是否在正确的位置上。

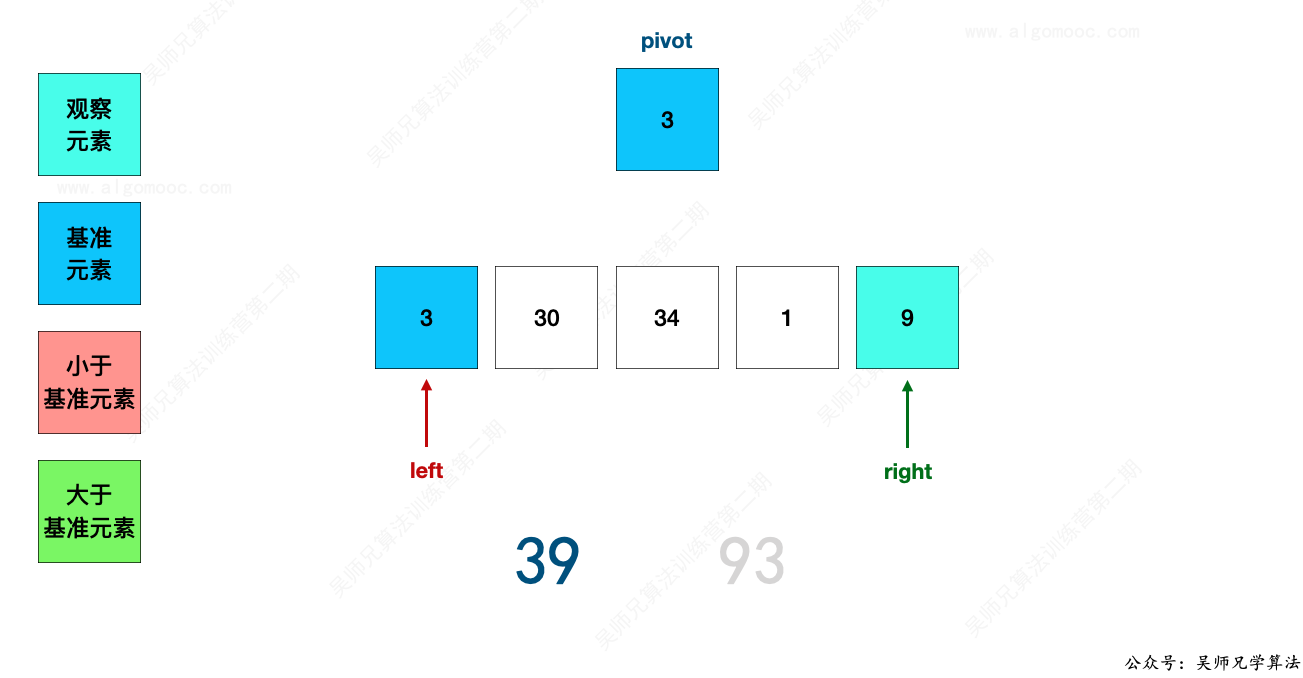
此时，39 < 93，说明 9 应该在基准值 3 的右边部分，而现在在右边部分，那么 9 就先不用去处理，继续看其它的数字。

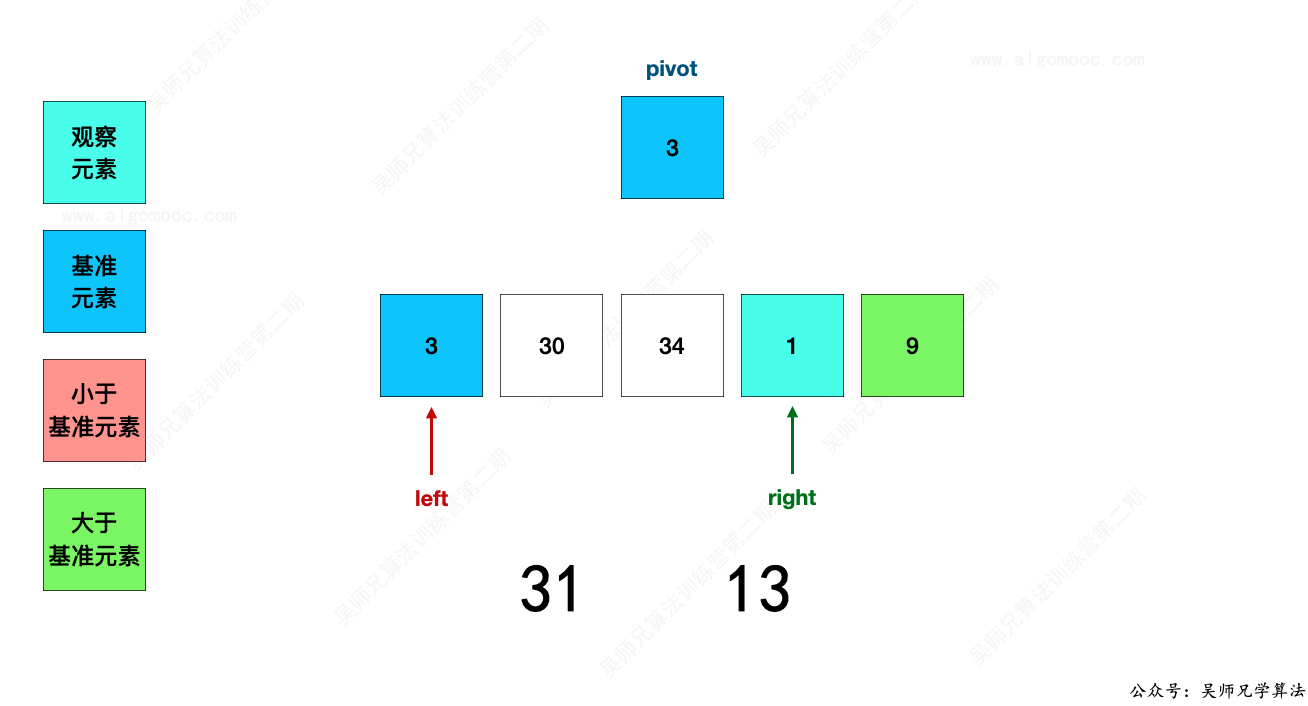
此时，31 > 13，说明 1 应该在基准值 3 的左边部分，而现在在右边部分，那么 1 应该挪到左边去，即挪到 left 指向的位置。

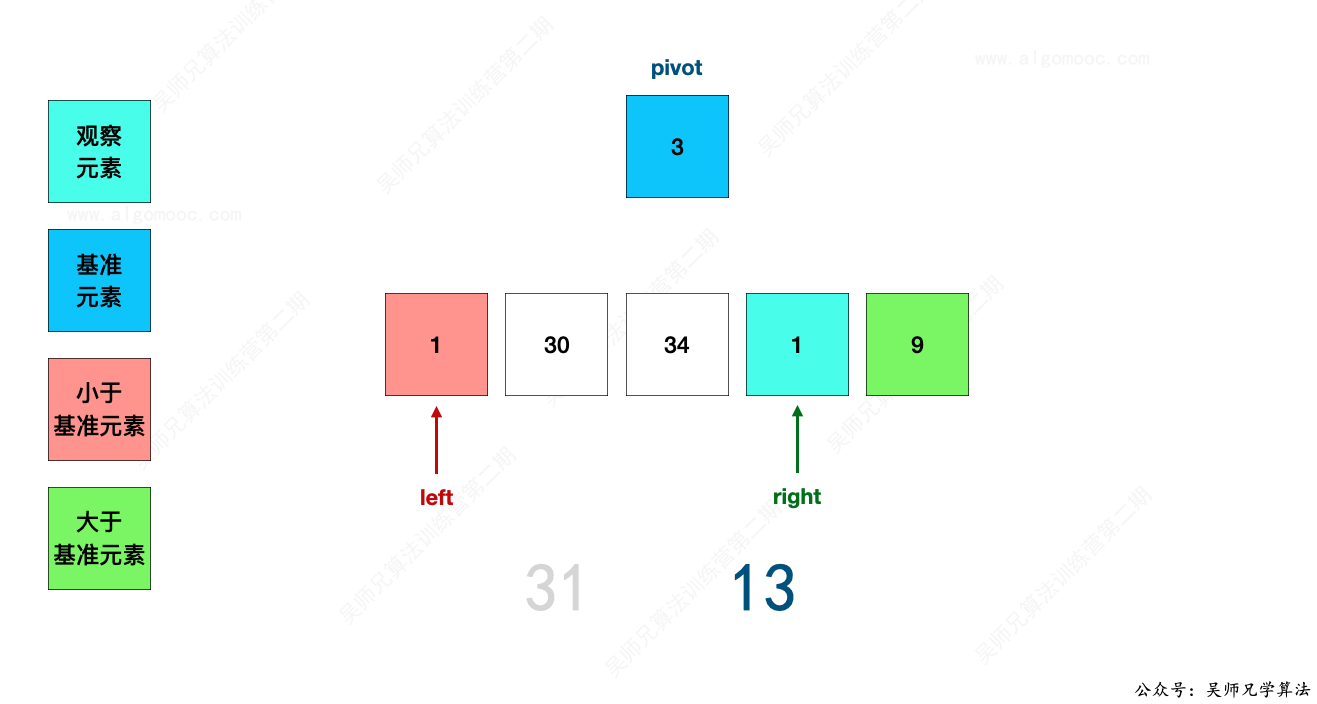
继续看其它的数字。

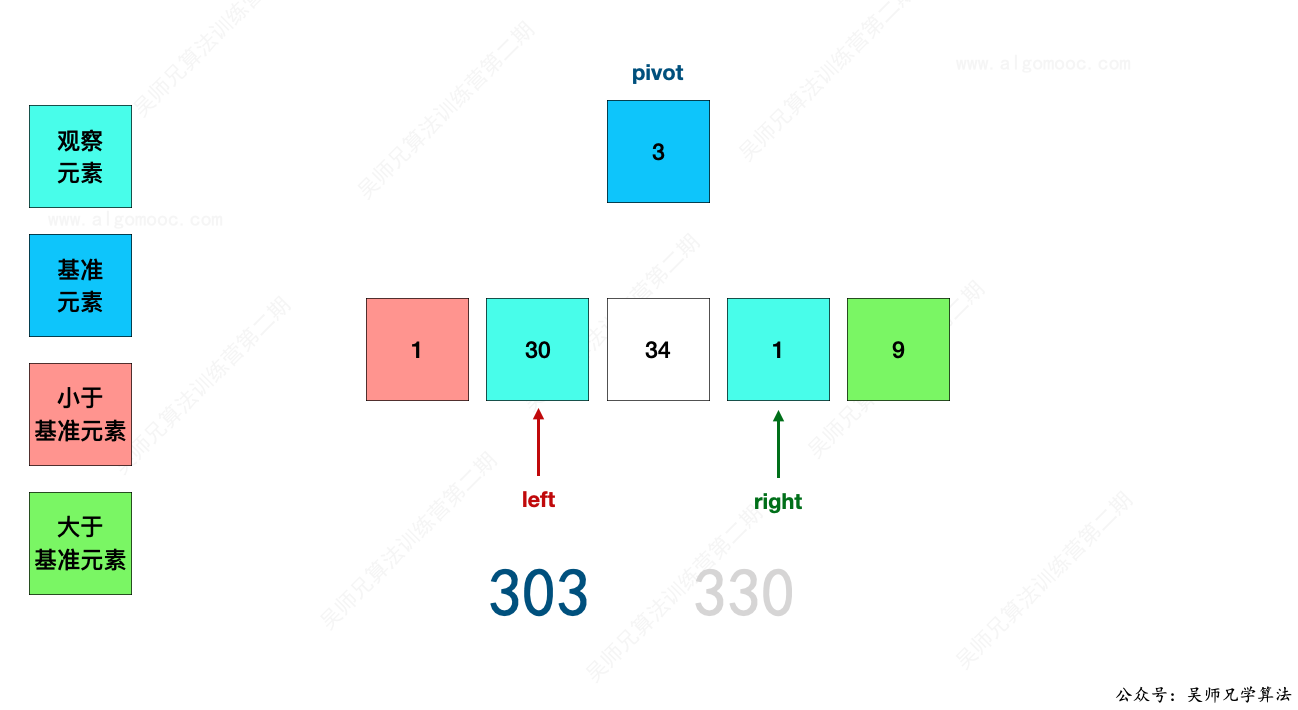
此时，303 < 330，说明 30 应该在基准值 3 的左边部分，而现在在左边部分，那么 30 就先不用去处理，继续看其它的数字。

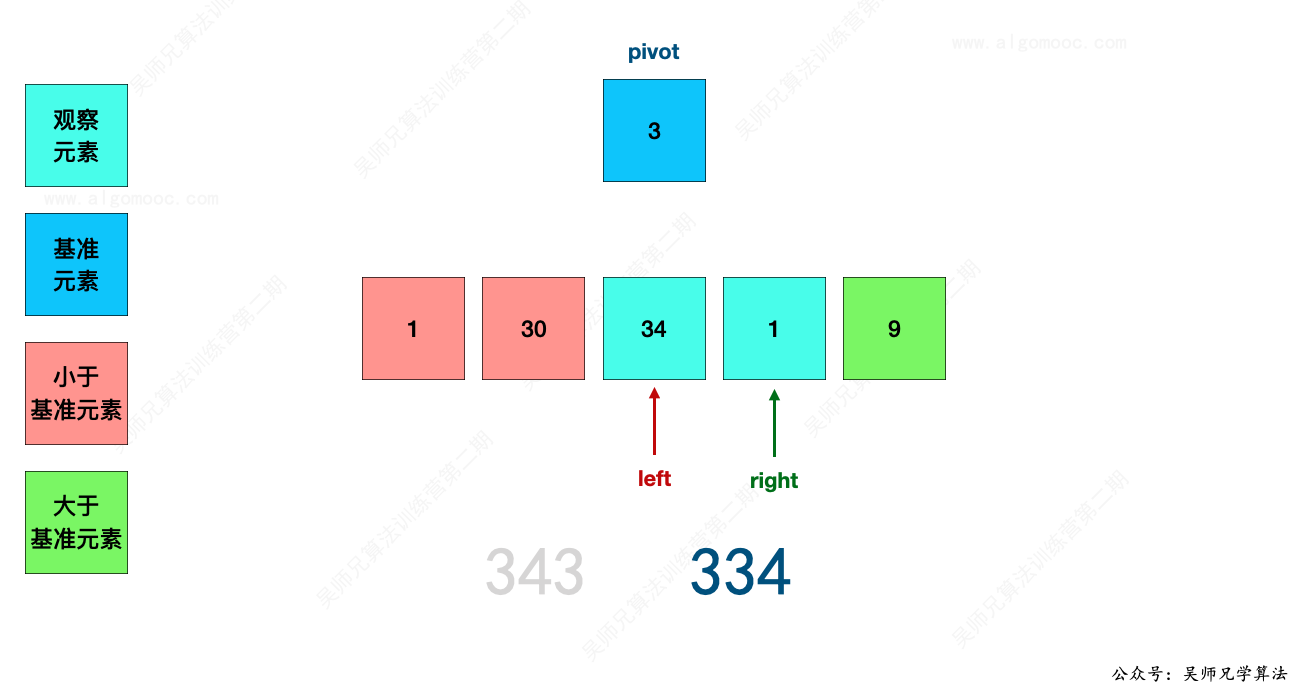
此时，343 > 334，说明 34 应该在基准值 3 的右边部分，而现在在左边部分，那么 34 应该挪到右边去，即挪到 right 指向的位置。

通过如上的操作之后，整个字符串数组被划分为了三个区域：红色、蓝色、绿色。

这样划分之后具备如下的特征：

1、红色区域的任意数字和蓝色区域的任意数字进行拼接，都是会小于蓝色区域的任意数字和红色区域的任意数字进行拼接。

比如 1 和 3 拼接的结果小于了 3 和 1 拼接的结果。

比如 30 和 3 拼接的结果小于了 3 和 30 拼接的结果。

2、蓝色区域的任意数字和绿色区域的任意数字进行拼接，都是会小于绿色区域的任意数字和蓝色区域的任意数字进行拼接。

比如 3 和 34 拼接的结果小于了 34 和 3 拼接的结果。

比如 3 和 9 拼接的结果小于了 9 和 3 拼接的结果。

接下来，我们只需要按照同样的方法把红色区域也划分为三个区域、绿色区域也划分为三个区域，就可以得到一个最小的数字。

为了帮助你更好的理解整个过程，我特意做了一组动画，点开可以查看：

三、参考代码

// 登录 AlgoMooc 官网获取更多算法图解
// https://www.algomooc.com
// 作者：程序员吴师兄
// 代码有看不懂的地方一定要私聊咨询吴师兄呀
// 剑指 Offer 45. 把数组排成最小的数:https://leetcode-cn.com/problems/ba-shu-zu-pai-cheng-zui-xiao-de-shu-lcof/
class Solution {
    public String minNumber(int[] nums) {
        
        // 先将 nums 转换为字符串数组的形式
        String[] strs = new String[nums.length];

        for(int i = 0; i < nums.length; i++){
            strs[i] = String.valueOf(nums[i]);
        }
        // 通过快速排序的方式，将字符串数组的每个字符按照约定的顺序进行排序
        quickSort(strs, 0, strs.length - 1);

        // 再把字符串数组转字符串的形式
        StringBuilder ans = new StringBuilder();

        for(String s : strs)
            ans.append(s);

        return ans.toString();
    }

    // 函数传入待排序数组 nums
    // 排序区间的左端点 left
    // 排序区间的右端点 right
    private void quickSort(String[] strs,int left, int right){

        // 如果 left 大于等于 right，说明该区间只有 1 个或者没有元素
        if( left >= right ){
            // 无需再递归划分后再排序，直接返回
            return;
        }

        // 调用函数 partition，将 left 和 right 之间的元素划分为左右两部分
        int mid = partition(strs,left,right);

        // 划分之后，再对 mid 左侧的元素进行快速排序
        quickSort(strs,left,mid - 1);

        // 划分之后，再对 mid 右侧的元素进行快速排序
        quickSort(strs,mid + 1,right);
    }

    // 直接套之前的快速排序的代码进行修改
    // 原先的小于的含义指的是数值上的小于，比如 1  < 10 
    // 但现在的小于含义为：a + b 拼凑的字符串小于 b + a 拼凑的字符串
    // 比如 a = 1 ，b = 10 
    // 那么 a + b = “110”，b + a = “101”
    // 显然，b + a < a + b
    // 也就是说 a 应该放到 b 的后面来拼凑字符串
    private int partition(String[] strs, int left ,int right){

        // 经典快速排序的写法
        // 设置当前区间的第一个元素为基准元素
        String pivot = strs[left];

        // left 向右移动，right 向左移动，直到 left 和 right 指向同一元素为止
        while( left < right ){

            // 当 pivot + strs[right] 的字符串小于 strs[right] + pivot 的字符串时
            // 说明 strs[right] 在正确的位置上，right 向左移动
            while( left < right && (pivot + strs[right]).compareTo(strs[right] + pivot) <= 0 ){
                // right 不断的向左移动
                right--;
            }

            // 此时，跳出了上面这个 while 循环，说明 pivot + strs[right] 的字符串大于 strs[right] + pivot 的字符串了
            // 说明 strs[right] 不在正确的位置上
            // 将此时的 strs[left] 赋值为 strs[right]
            // 执行完这个操作，比 pivot 小的这个元素被移动到了左侧
            strs[left] = strs[right];

            // 当 strs[left] + pivot 的字符串小于 pivot + strs[left] 的字符串时
            // 说明 strs[left] 在正确的位置上，left 向右移动
            while( left < right && (strs[left] + pivot).compareTo(pivot + strs[left]) <= 0){
                // left 不断的向右移动
                left++;
            }

            // 此时，跳出了上面这个 while 循环，说明 strs[left] + pivot 的字符串大于 pivot + strs[left] 的字符串了
            // 说明 strs[left] 不在正确的位置上
            // 将此时的 strs[right] 赋值为 strs[left]
            // 执行完这个操作，比 pivot 大的这个元素被移动到了右侧
            strs[right] = strs[left];

        }

        // 此时，left 和 right 相遇，那么需要将此时的元素设置为 pivot
        // 这个时候，pivot 的左侧元素都小于它，右侧元素都大于它
        strs[left] = pivot;

        // 返回 left
        return left;

    }
}